Définition de la continuité à l’aide des ensembles ouverts

Une fonction \( f : X \to Y \) est continue si, et seulement si, pour tout point \( x \in X \) et tout ouvert \( U \subset Y \) contenant \( f(x) \), il existe un voisinage \( V \) de \( x \) tel que \( f(V) \subset U \).

En d’autres termes, une fonction \( f : X \to Y \) est continue lorsque, pour tout ouvert \( U \subset Y \), l’image réciproque \( f^{-1}(U) \) est un ouvert de \( X \).

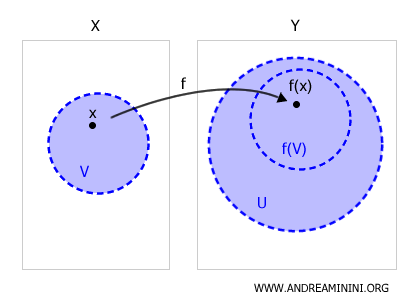
Autrement dit, l’image réciproque de tout ouvert du codomaine est un ouvert dans le domaine.

Ce théorème fournit une définition topologique de la continuité, fondée sur la structure des ouverts dans les deux espaces.

On parle également de définition de la continuité par les ensembles ouverts.

Remarque : Ce résultat est aussi appelé équivalence des définitions de la continuité, car il établit l’équivalence entre deux formulations classiques : la définition topologique par les ouverts, et la définition analytique par le couple \(\varepsilon\)-\(\delta\). La définition analytique s’énonce ainsi : "Une fonction \( f \) est continue en un point \( x_0 \in \mathbb{R} \) si, pour tout \(\varepsilon > 0\), il existe un \(\delta > 0\) tel que, pour tout \( x \in \mathbb{R} \), si \( |x - x_0| < \delta \), alors \( |f(x) - f(x_0)| < \varepsilon \)", une formulation introduite dans les premiers cours de calcul différentiel.

On peut également caractériser la continuité à l’aide des ensembles fermés : une fonction est continue si l’image réciproque de tout fermé est elle aussi un fermé.

En effet, pour une fonction \( f : X \to Y \) entre espaces topologiques, \( f \) est continue si, et seulement si, pour tout fermé \( C \subset Y \), l’ensemble \( f^{-1}(C) \) est fermé dans \( X \).

Ce résultat montre que la continuité peut s’exprimer aussi bien à l’aide des ouverts que des fermés, ces deux notions étant complémentaires et profondément liées en topologie.

Un exemple concret

Considérons la fonction \( f : \mathbb{R} \to \mathbb{R} \) définie par \( f(x) = x^2 \).

Nous souhaitons en vérifier la continuité en utilisant la définition topologique fondée sur les ensembles ouverts.

Selon cette définition, \( f \) est continue si, pour tout ouvert \( U \subset \mathbb{R} \) et tout \( x \in f^{-1}(U) \), il existe un voisinage \( V \) de \( x \) tel que \( f(V) \subset U \).

Prenons par exemple l’ouvert \( U = (1, 4) \), qui contient tous les réels strictement compris entre 1 et 4.

Déterminons \( f^{-1}(U) \), c’est-à-dire les \( x \in \mathbb{R} \) tels que \( x^2 \in (1, 4) \).

Nous cherchons les solutions de l’inéquation :

$$ 1 < x^2 < 4 $$

Ce qui équivaut à :

$$ 1 < |x| < 2 $$

Autrement dit, \( x \in (-2, -1) \cup (1, 2) \), un ensemble manifestement ouvert dans \( \mathbb{R} \).

Nous avons donc identifié \( f^{-1}(U) \) comme un ouvert.

Choisissons un point quelconque \( x \in f^{-1}(U) \), par exemple \( x = 1{,}5 \).

On a \( f(1{,}5) = 2{,}25 \), qui appartient à \( U = (1, 4) \).

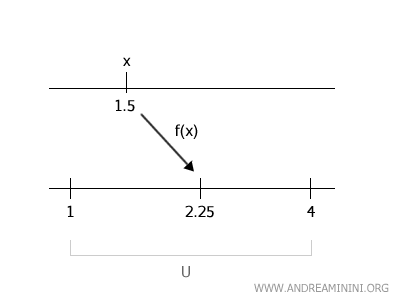
Recherchons un voisinage \( V \) de \( x = 1{,}5 \) tel que \( f(V) \subset (1, 4) \).

Par exemple, prenons l’intervalle \( V = (1{,}4, 1{,}6) \).

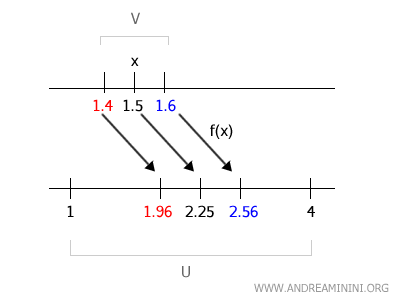
Calculons les extrémités de l’image de ce voisinage :

$$ f(1{,}4) = 1{,}96 \quad \text{et} \quad f(1{,}6) = 2{,}56 $$

On en déduit que \( f(V) = (1{,}96, 2{,}56) \subset (1, 4) = U \).

Cela confirme que, pour tout \( x \in f^{-1}(U) \), il existe un voisinage \( V \) de \( x \) tel que \( f(V) \subset U \), ce qui satisfait la condition de continuité.

Comme cette propriété est vérifiée pour tout \( x \in \mathbb{R} \), on conclut que la fonction \( f(x) = x^2 \) est continue sur tout \( \mathbb{R} \).

Remarque : Pour qu’une fonction soit continue, cette propriété doit être vérifiée en tout point \( x \in X \), et non en un seul. La continuité est une propriété globale qui doit s’appliquer sur l’ensemble du domaine. Dans le cas de \( f : \mathbb{R} \to \mathbb{R} \), il faut démontrer que, pour tout \( x \in \mathbb{R} \) et tout ouvert \( U \) contenant \( f(x) \), il existe un voisinage \( V \) de \( x \) tel que \( f(V) \subset U \).

Démonstration

Nous allons diviser la démonstration en deux étapes :

A] Première étape

Supposons que la fonction \( f \) soit continue au sens topologique.

Soit \( x \in X \) et un ouvert \( U \subset Y \) tel que \( f(x) \in U \).

Posons \( V = f^{-1}(U) \), c’est-à-dire l’ensemble des points de \( X \) dont l’image par \( f \) est contenue dans \( U \).

Comme \( f \) est continue, \( V \) est un ouvert de \( X \).

Comme \( x \in V \) et \( f(V) \subset U \), la condition est bien remplie : pour tout ouvert contenant \( f(x) \), il existe un voisinage ouvert de \( x \) dont l’image est incluse dans celui-ci.

B] Deuxième étape

Supposons maintenant que, pour tout \( x \in X \) et tout ouvert \( U \subset Y \) contenant \( f(x) \), il existe un voisinage \( V \) de \( x \) tel que \( f(V) \subset U \).

Nous voulons démontrer que, pour tout ouvert \( W \subset Y \), l’antécédent \( f^{-1}(W) \) est ouvert dans \( X \).

Soit \( x \in f^{-1}(W) \), autrement dit \( f(x) \in W \).

D’après l’hypothèse, il existe un voisinage \( V_x \) de \( x \) tel que \( f(V_x) \subset W \).

On en déduit que \( V_x \subset f^{-1}(W) \), donc \( f^{-1}(W) \) contient un voisinage ouvert autour de chacun de ses points.

Comme c’est vrai pour tout \( x \in f^{-1}(W) \), on en conclut que \( f^{-1}(W) \) est un ouvert de \( X \).

Conclusion

En définitive, les définitions de la continuité fondées sur les ensembles ouverts et sur les voisinages sont parfaitement équivalentes.

Et ainsi de suite.