Ensembles ni ouverts ni fermés
En topologie, un ensemble qui n’est ni ouvert ni fermé ne satisfait pas aux critères permettant de le classer dans l’une ou l’autre de ces deux catégories.
Cette situation peut survenir dans une topologie où l’ensemble considéré n’est défini ni comme un ensemble ouvert, ni comme le complémentaire d’un tel ensemble.
Par conséquent, un tel ensemble ne peut pas non plus être qualifié d’ensemble fermé.
Remarque : Dans la topologie usuelle des nombres réels, il peut sembler peu intuitif d’imaginer des ensembles qui ne soient ni ouverts ni fermés. Toutefois, dans des structures topologiques plus générales, leur existence est parfaitement naturelle. Un exemple concret permettra de mieux saisir cette notion.
Exemple concret
Supposons que l’on considère l’ensemble \( X = \{a,b,c,d\} \) et une topologie \( T \) définie par les ensembles ouverts suivants : \( \{b\} \), \( \{a,b\} \), \( \{c,d\} \), \( \{b,c,d\} \), \( \{a,b,c,d\} \) et l’ensemble vide (Ø).
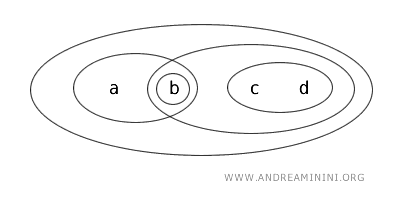
Intéressons-nous maintenant au sous-ensemble \( \{b,c\} \) de \( X \).
- L’ensemble \( \{b,c\} \) n’est pas ouvert dans la topologie \( T \), car il ne figure pas explicitement parmi les ensembles ouverts définis.
- De même, \( \{b,c\} \) n’est pas fermé non plus, car son complémentaire \( X \setminus \{b,c\} = \{a,d\} \) n’appartient pas à la collection des ensembles ouverts de \( T \).
En définitive, dans la topologie \( T \), l’ensemble \( \{b,c\} \) n’est ni ouvert ni fermé.
Et ainsi de suite.