Transformations topologiques

Les transformations topologiques sont des opérations appliquées aux espaces topologiques pour en préserver des propriétés essentielles comme la connectivité et la continuité.

Ces transformations jouent un rôle crucial dans l'étude de la topologie, un domaine mathématique qui s'intéresse aux propriétés des espaces restant invariantes sous des transformations continues.

Voici quelques caractéristiques fondamentales des transformations topologiques :

• Continuité
  Une transformation topologique doit être continue, ce qui implique que de petites variations des données initiales entraînent de faibles modifications des résultats.
• Connectivité et proximité
  Les transformations topologiques préservent les notions de proximité et de connectivité. Ainsi, si deux points sont proches ou reliés dans l'espace original, ils le resteront dans l'espace transformé.
• Déformation sans déchirure ni collage
  Les objets peuvent être étirés, comprimés ou courbés, mais ils ne doivent ni être déchirés ni collés. Par exemple, un beignet peut se transformer en tasse de café à travers une transformation topologique, les deux contenant un unique "trou".

Applications : Les transformations topologiques trouvent leur utilité dans divers domaines, allant des mathématiques pures comme la théorie des nœuds et la topologie algébrique à l'étude des propriétés invariantes des objets sous déformations continues.

Types de transformations topologiques

En topologie, on catégorise généralement les transformations selon leur capacité à conserver certaines propriétés topologiques.

Voici quelques types fondamentaux de transformations topologiques :

• Homéomorphismes
  Un homéomorphisme est une transformation continue qui dispose d'un inverse continu. Fondamentalement, cela permet de transformer un espace en un autre et de revenir en arrière sans bris ni collage. Ces transformations sont essentielles en topologie. Par exemple, transformer une tasse en un beignet, comme mentionné précédemment.
• Isotopies
  Une isotopie est une forme spécifique d'homéomorphisme où chaque étape de la transformation est elle-même un homéomorphisme. Par exemple, le déplacement d'un nœud le long d'une corde sans le serrer ni le relâcher, chaque phase de mouvement constitue une isotopie.
• Homotopies
  Ces transformations montrent comment une fonction peut être "déformée" en une autre tout en préservant certaines propriétés topologiques. L'homotopie est moins restrictive que l'homéomorphisme. Par exemple, étirer un ressort puis le relâcher, les différentes configurations lors de l'extension et du relâchement étant des homotopies.
• Difféomorphismes
  Un difféomorphisme est un homéomorphisme qui est également différentiable. C'est particulièrement pertinent en topologie différentielle, où la lissité et la différentiabilité des surfaces sont essentielles. Par exemple, transformer une sphère extensible en un ellipsoïde allongé.

Ces types de transformations mettent l'accent sur différents aspects de la continuité et de la capacité de déformation des espaces et des fonctions en topologie.

Leur application varie en fonction du contexte spécifique dans lequel elles sont utilisées, que ce soit en topologie générale, algébrique ou différentielle.

Différences entre transformations géométriques et topologiques

Les transformations géométriques et topologiques diffèrent par leurs propriétés et leurs applications :

• Transformations géométriques
  Les transformations géométriques mod ifient les objets dans l'espace en conservant des propriétés géométriques telles que les distances, les angles et les formes. Exemples de telles transformations : translations, rotations, réflexions et échelles.

  Par exemple, une rotation conserve les distances et les angles mais change l'orientation.

• Transformations topologiques
  Les transformations topologiques modifient les espaces tout en conservant des propriétés topologiques telles que la connectivité et la continuité, sans nécessairement préserver les distances ou les angles. Elles permettent une grande flexibilité, autorisant l'étirement et la déformation des figures sans les découper ni les coller.

  Par exemple, en topologie, un beignet peut se transformer en tasse de café car tous deux possèdent un unique trou.

Alors que les transformations géométriques se concentrent sur les déplacements ou les changements de forme des objets en préservant des mesures et proportions spécifiques, les transformations topologiques mettent l'accent sur les déformations d'espaces qui préservent la connectivité et la continuité, indépendamment de la forme ou de la taille exactes.

Peut-on avoir des transformations à la fois géométriques et topologiques ?

Oui, certaines transformations modifient les objets en conservant des propriétés géométriques telles que les angles, les longueurs et les formes, tout en étant continues et en préservant des propriétés topologiques comme la connectivité et la continuité.

Voici quelques exemples concrets :

• Isométries
  Les isométries, telles que les translations, rotations et réflexions, préservent des propriétés comme les distances entre les points et les angles, ce qui les rend à la fois des transformations géométriques et topologiques. Elles sont spécifiquement des homéomorphismes, car elles comportent également un inverse continu.
  
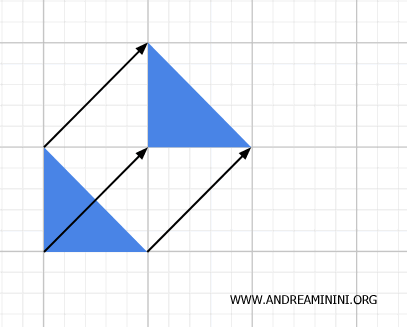
• Similarités
  Les similarités modifient la taille de l'objet mais conservent la forme, y compris les dilatations ou contractions qui maintiennent les angles et les proportions relatives. Ces transformations sont géométriques de par leur impact sur la forme et la taille, mais également topologiques car elles sont continues et préservent la connectivité.

Ces transformations illustrent que les propriétés géométriques et topologiques ne sont pas toujours distinctes. Dans certains cas, une transformation peut être à la fois géométriquement significative et topologiquement valide.

Et ainsi de suite.