Graphe topologique
Un graphe topologique est un espace topologique construit à partir d’un ensemble fini de points, appelés « sommets », et d’un ensemble fini d’intervalles fermés, deux à deux disjoints, dans \(\mathbb{R}\), appelés « arêtes ». Ces arêtes sont reliées aux sommets selon des règles de connexions bien définies.
La topologie de l’espace ainsi formé dépend entièrement de la manière dont ces connexions sont établies. Elle confère au graphe une double nature - à la fois géométrique et topologique - qui exprime la structure des relations entre les sommets.
Ce procédé permet donc de construire un espace topologique représentant fidèlement l’architecture d’un graphe.
Remarque : Il s’agit d’un cas particulier de topologie quotient, dans lequel on munit un espace d’une topologie pour en former un autre, appelé « espace induit ». Ce nouvel espace est obtenu en reliant un ensemble d’intervalles à un ensemble de sommets. Autrement dit, on part d’éléments simples (des intervalles fermés) que l’on transforme en les identifiant à certains points, afin d’engendrer une structure topologique plus complexe.
Construction d’un graphe topologique
La construction d’un graphe topologique peut être décrite en deux étapes fondamentales :
- Sommets : on commence par un ensemble fini de points, appelés sommets. Par exemple, on peut les noter A, B, C, D, E et F.
- Arêtes : on considère ensuite un ensemble d’intervalles (segments), chacun possédant deux extrémités. Ces extrémités sont alors « collées » à certains sommets, ce qui établit les connexions. Ces segments deviennent ainsi des arêtes du graphe.
Autrement dit, il s’agit de relier des intervalles à des sommets de manière contrôlée pour former une structure appelée graphe.
On qualifie cette construction de « topologique » car elle repose sur le mode d’assemblage des différents sous-espaces constituants.
Exemple illustratif
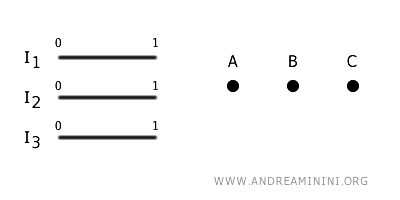
Considérons trois intervalles fermés distincts de \(\mathbb{R}\) :
$$ I_1 = [0, 1], \quad I_2 = [0, 1], \quad I_3 = [0, 1] $$
Ce sont de simples segments dont les extrémités sont les points \(0\) et \(1\).
Définissons ensuite un ensemble \( G \) constitué de trois sommets, que nous appellerons \(A\), \(B\) et \(C\) :
$$ G = \{ A, B, C \} $$
Ces sommets représentent les points auxquels viendront s’attacher les extrémités des intervalles.
Nous appliquons maintenant le principe de la topologie quotient, en identifiant les extrémités des intervalles à des sommets spécifiques :
- L’extrémité \(0\) de \(I_1\) est identifiée à \(A\), et l’extrémité \(1\) à \(B\).
- L’extrémité \(0\) de \(I_2\) est identifiée à \(B\), et l’extrémité \(1\) à \(C\).
- L’extrémité \(0\) de \(I_3\) est identifiée à \(A\), et l’extrémité \(1\) à \(C\).
On obtient ainsi un graphe composé de trois sommets \(A\), \(B\), \(C\), et de trois arêtes reliant respectivement : \( (A, B) \), \( (B, C) \) et \( (A, C) \).
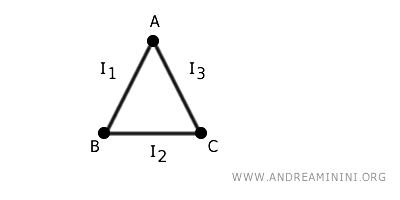
En partant d’intervalles disjoints et en reliant leurs extrémités à des sommets, on construit ainsi une nouvelle entité : le graphe topologique.
En somme, construire un graphe topologique consiste à assembler des intervalles autour de sommets choisis de façon à modéliser une structure relationnelle.
Ce procédé peut naturellement être généralisé à des graphes beaucoup plus complexes, intégrant un nombre plus élevé de sommets et d’arêtes.