Homéomorphismes en topologie

Un homéomorphisme est une transformation topologique qui consiste en une fonction à la fois bijective et continue, accompagnée de son inverse également continu.

De façon plus imagée, cela permet de transformer un espace en un autre, puis de revenir à l'état initial sans rupture ni ajout.

Pour faire simple, un homéomorphisme permet de passer d'un espace à un autre de manière fluide et sans altération.

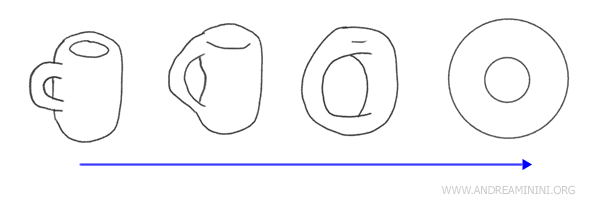
Considérons, par exemple, une tasse à café avec une anse et un beignet (tore) - ces objets sont homéomorphes en topologie. En effet, il est possible de déformer l'un en l'autre continuellement et réciproquement.

Sur le plan topologique, ces formes sont équivalentes car elles comportent toutes les deux un seul « trou » - le trou central du beignet et l'espace de l'anse de la tasse. Vous pourriez modeler la tasse autour de son anse pour lui donner la forme d'un beignet.

Lorsque deux espaces topologiques sont reliés par un homéomorphisme, ils sont qualifiés d'« espaces homéomorphes », ce qui signifie que, du point de vue topologique, ils sont fondamentalement identiques, bien que leurs formes géométriques puissent varier.

Caractéristiques d’un homéomorphisme

Voici quelques propriétés fondamentales qui caractérisent un homéomorphisme :

• Application bijective
  Elle met en correspondance, de manière unique, chaque élément d’un espace avec un élément de l’autre, et réciproquement.
• Continuité
  Par nature, un homéomorphisme est une application continue : de petites variations de l’entrée produisent de petites variations de la sortie.
• Application réciproque continue
  L’inverse de l’application doit également être continue, ce qui garantit la réversibilité de la transformation sans rupture de continuité.
• Conservation des propriétés topologiques
  Un homéomorphisme préserve les propriétés topologiques essentielles telles que la continuité, la connexité ou la compacité. Ainsi, les relations internes de l’espace d’origine sont intactes dans l’espace transformé.

En somme, un homéomorphisme est une application continue et bijective entre deux espaces topologiques \(X\) et \(Y\), dont l’inverse est également continue. Cela permet de conserver les propriétés topologiques des deux espaces.

Pour le dire simplement, un homéomorphisme permet de “reconfigurer” un espace en un autre sans le déchirer ni le recoller : c’est une forme d’« équivalence topologique parfaite » entre deux structures spatiales.

Rappelons la définition topologique de la continuité :

Soient \(X\) et \(Y\) deux espaces topologiques. Une application \(f : X \to Y\) est dite continue si, pour tout ouvert \(V\) de \(Y\), l’image réciproque \(f^{-1}(V)\) est un ouvert de \(X\).

Autrement dit, une application continue en topologie conserve la structure des ouverts lorsqu’on passe d’un espace à l’autre.

La notion de continuité en topologie est donc plus abstraite et générale que celle définie en analyse.

Remarque : En analyse, la continuité repose sur la distance entre les points. En topologie, en revanche, elle s’appuie uniquement sur la structure des ouverts, sans référence à une distance.

Un exemple concret

Illustrons de façon claire et intuitive les idées de continuité et d’homéomorphisme à travers des ensembles ouverts.

Considérons deux espaces topologiques : \(X = \{a, b, c, d\}\) et \(Y = \{1, 2\}\).

• Dans l’espace \(X\), les ouverts sont : \(\{\}, \{a\}, \{a, b\}, \{a, b, c, d\}\).
• Dans l’espace \(Y\), les ouverts sont : \(\{\}, \{1\}, \{1, 2\}\).

Une application \(f : X \to Y\) est continue si, pour chaque ouvert de \(Y\), son image réciproque est un ouvert de \(X\).

Définissons l’application \(f\) ainsi :

\(f(a) = 1\), \(f(b) = 1\), \(f(c) = 2\), \(f(d) = 2\).

Pour faciliter la compréhension, nous représenterons l’application \(f\) et les espaces topologiques en entourant les ensembles ouverts avec des cercles.

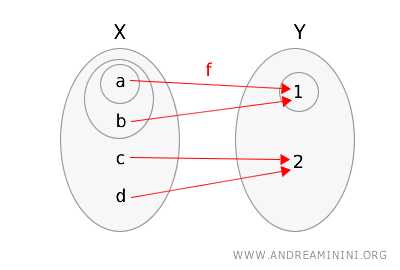
Vérifiant la définition topologique de la continuité :

• L’ouvert \(\{1\}\) de \(Y\) a pour image réciproque \(f^{-1}(\{1\}) = \{a, b\}\), qui est un ouvert dans \(X\).
• L’ouvert \(\{1, 2\}\) de \(Y\) a pour image réciproque \(f^{-1}(\{1, 2\}) = \{a, b, c, d\}\), qui est également ouvert dans \(X\).

Puisque l’image réciproque de chaque ouvert de \(Y\) est un ouvert de \(X\), l’application \(f\) est continue.

Remarque : L’ensemble vide n’est pas pris en compte car, par définition, il est ouvert dans tout espace topologique.

Voyons maintenant une autre application \(g : X \to Y\), définie par :

\(g(a) = 1\), \(g(b) = 1\), \(g(c) = 1\), \(g(d) = 2\).

Nous représenterons également cette application en encerclant les ouverts dans chaque espace.

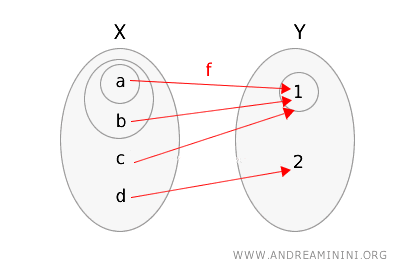
Vérification de la continuité :

• L’ouvert \(\{1\}\) de \(Y\) a pour image réciproque \(g^{-1}(\{1\}) = \{a, b, c\}\), qui n’est pas un ouvert de \(X\).

Comme il existe un ouvert de \(Y\) dont l’image réciproque n’est pas ouverte dans \(X\), l’application \(g\) n’est pas continue.

Remarque : Pour résumer, une application est continue si l’image réciproque de tout ouvert de l’espace d’arrivée (\(Y\)) est un ouvert de l’espace de départ (\(X\)). Dans le premier exemple, la fonction \(f\) est continue car cette condition est toujours remplie. En revanche, la fonction \(g\) ne l’est pas, car elle ne satisfait pas cette condition pour tous les ouverts.

Définition d’un homéomorphisme

Soient deux espaces topologiques \( X \) et \( Y \), et une application bijective \( f : X \to Y \) admettant un inverse \( f^{-1} : Y \to X \). Si \( f \) et \( f^{-1} \) sont toutes deux continues, on dit que \( f \) est un homéomorphisme, et que les espaces \( X \) et \( Y \) sont homéomorphes, autrement dit \( X \cong Y \).

On appelle aussi ces espaces équivalents du point de vue topologique.

Que cela signifie-t-il concrètement ?

Deux espaces sont homéomorphes ou topologiquement équivalents lorsqu’ils partagent la même structure fondamentale du point de vue topologique, même si leur forme géométrique peut être très différente.

Un homéomorphisme se caractérise par trois propriétés essentielles :

1. Bijectivité : L’application \( f : X \to Y \) est à la fois injective et surjective. Chaque point de \( X \) correspond à un point unique de \( Y \), et réciproquement.
2. Continuité de \( f \) : L’application est continue si l’image réciproque de tout ouvert de \( Y \) est un ouvert dans \( X \).
3. Continuité de \( f^{-1} \) : L’inverse \( f^{-1} : Y \to X \) doit lui aussi être continu, c’est-à-dire que l’image réciproque de tout ouvert de \( X \) est un ouvert dans \( Y \).

Exemple : Imaginez une feuille de papier que l’on enroule pour former un cylindre. Le cylindre et la feuille plane sont homéomorphes car on peut passer de l’un à l’autre sans couper ni recoller - il suffit de dérouler ou d’enrouler. Bien que leur forme géométrique diffère, leur structure topologique (c’est-à-dire les ouverts) reste inchangée.

Il est important de noter que le fait qu’une application bijective \( f \) soit continue ne garantit pas la continuité de son inverse \( f^{-1} \), sauf si \( f \) est également une application ouverte.

Autrement dit, une fonction continue et bijective n’est pas nécessairement un homéomorphisme si son inverse n’est pas continue.

En topologie, on dit qu’une application \( f : X \to Y \) est continue lorsque l’image réciproque de tout ouvert de \( Y \) est un ouvert de \( X \).

Mais cela ne signifie pas que l’image directe d’un ouvert de \( X \) est nécessairement ouverte dans \( Y \).

Pour que \( f^{-1} \) soit continue, il faut donc que \( f \) soit non seulement continue et bijective, mais aussi une application ouverte.

Exemple

Considérons les espaces topologiques suivants :

• \( X = (a, b) \), muni de la topologie \( T_X = \{\emptyset, \{a\}, \{b\}, X\} \).
• \( Y = (1, 2) \), muni de la topologie \( T_Y = \{\emptyset, Y\} \).

Définissons une application \( f : X \to Y \) par \( f(a) = 1 \) et \( f(b) = 2 \).

Cette application est clairement bijective : chaque élément de \( X \) est associé à un élément unique de \( Y \), et réciproquement.

Remarque : Dans le schéma, les ouverts sont indiqués par des cercles. Dans \( X \), les ensembles \{a\}, \{b\} et \{a, b\} sont ouverts ; dans \( Y \), seul \{1, 2\} est ouvert. Les ensembles vides, toujours ouverts par définition, ne sont pas représentés ici.

Étudions maintenant la continuité de \( f \) et de son inverse \( f^{-1} \).

• Continuité de \( f \)
  La topologie \( T_Y \) contient seulement \( \emptyset \) et \( Y \). On a :
  • \( f^{-1}(\emptyset) = \emptyset \), qui est ouvert dans \( T_X \)
  • \( f^{-1}(Y) = X \), ouvert dans \( T_X \)
  L’application \( f \) est donc continue.
• Continuité de \( f^{-1} \)
  Examinons maintenant \( f^{-1} : Y \to X \), avec \( f^{-1}(1) = a \) et \( f^{-1}(2) = b \). Considérons les ouverts de \( X \) :
  • \( f^{-1}(\emptyset) = \emptyset \), ouvert dans \( T_Y \)
  • \( f^{-1}(\{a\}) = \{1\} \), qui n’est pas ouvert dans \( T_Y \)
  • \( f^{-1}(\{b\}) = \{2\} \), non plus
  • \( f^{-1}(X) = Y \), ouvert dans \( T_Y \)
  Certaines préimages ne sont pas ouvertes, donc \( f^{-1} \) n’est pas continue.

En conclusion, bien que \( f \) soit bijective et continue, son inverse ne l’est pas. \( f \) n’est donc pas un homéomorphisme.

Cet exemple illustre que la continuité d’une application et sa bijectivité ne suffisent pas à garantir la continuité de son inverse.

Remarque : L’absence de continuité de \( f^{-1} \) est due à la différence entre les topologies : celle de \( X \) est plus fine (plus riche en ouverts) que celle de \( Y \), qui est plus grossière.

Exemple 2

Considérons maintenant un autre exemple avec des topologies différentes :

• \( X = (a, b) \), muni de \( T_X = \{\emptyset, \{a\}, X\} \).
• \( Y = (1, 2) \), muni de \( T_Y = \{\emptyset, \{1\}, Y\} \).

Définissons \( f : X \to Y \) par \( f(a) = 1 \), \( f(b) = 2 \).

L’application \( f \) est de nouveau bijective.

Voyons si \( f \) et \( f^{-1} \) sont continues.

• Continuité de \( f \)
  Les ouverts de \( Y \) sont \( \emptyset \), \(\{1\}\) et \( Y \) :
  • \( f^{-1}(\emptyset) = \emptyset \), ouvert dans \( T_X \)
  • \( f^{-1}(\{1\}) = \{a\} \), ouvert dans \( T_X \)
  • \( f^{-1}(Y) = X \), ouvert dans \( T_X \)
  Toutes les préimages sont ouvertes, donc \( f \) est continue.
• Continuité de \( f^{-1} \)
  Les ouverts de \( X \) sont \( \emptyset \), \(\{a\}\) et \( X \) :
  • \( f^{-1}(\emptyset) = \emptyset \), ouvert dans \( T_Y \)
  • \( f^{-1}(\{a\}) = \{1\} \), ouvert dans \( T_Y \)
  • \( f^{-1}(X) = Y \), également ouvert dans \( T_Y \)
  L’inverse \( f^{-1} \) est donc aussi continue.

On en déduit que \( f \) est bijective, continue, et que son inverse l’est aussi. Par conséquent, \( f \) est un homéomorphisme.

La différence avec le premier exemple réside dans le choix des topologies, ici mieux harmonisées.

Remarque : Cet exemple montre que, pour garantir la continuité de l’inverse et donc l’existence d’un homéomorphisme, il est essentiel de choisir des topologies compatibles sur \( X \) et \( Y \).

Différenciation entre homéomorphismes et autres transformations topologiques

Bien que le terme « homéomorphisme » soit parfois utilisé de façon générique pour désigner les transformations topologiques, il désigne en réalité une classe particulière parmi celles-ci.

Les homéomorphismes et les transformations topologiques sont intimement liés, mais ils ne recouvrent pas exactement les mêmes notions :

• Transformations topologiques
  Ce terme renvoie à une catégorie générale d'applications entre espaces topologiques qui préservent certaines propriétés fondamentales, comme la continuité, la connexité ou la compacité. Cette classe englobe les homéomorphismes, mais aussi d’autres transformations notables, telles que les isotopies, les homotopies et les difféomorphismes.
• Homéomorphismes
  Il s'agit d'applications bijectives et continues dont l'inverse est également continue. Elles établissent une correspondance réciproque entre deux espaces en préservant entièrement leur structure topologique. Deux espaces reliés par un homéomorphisme sont donc topologiquement indiscernables, même si leurs formes géométriques peuvent être très différentes.

En résumé, tout homéomorphisme est une transformation topologique, mais l'inverse n'est pas toujours vrai : toutes les transformations topologiques ne satisfont pas aux critères requis pour être des homéomorphismes.

Certaines applications, bien qu'elles préservent des propriétés topologiques essentielles, présentent des particularités ou des restrictions qui les excluent de la définition stricte d'un homéomorphisme.

Remarques complémentaires

Voici quelques précisions utiles pour mieux comprendre le rôle et les implications des homéomorphismes :

• Propriété topologique
  Une propriété topologique est une caractéristique intrinsèque d’un espace qui demeure inchangée par homéomorphisme. Autrement dit, si deux espaces sont homéomorphes (liés par une application continue, bijective et dont l’inverse est continue), alors ils partagent exactement les mêmes propriétés topologiques.
• Théorème de Hausdorff sur les homéomorphismes
  Ce théorème stipule que si \( f : X \to Y \) est un homéomorphisme et que \( X \) est un espace de Hausdorff, alors \( Y \) l’est aussi. Autrement dit, puisque les homéomorphismes préservent les propriétés topologiques, la propriété de séparation des points propre à Hausdorff se transmet de \( X \) à \( Y \).
• L’analogue du concept d’homéomorphisme en algèbre est l’isomorphisme de groupes. Tandis qu’un isomorphisme conserve la structure algébrique d’un objet, un homéomorphisme conserve la structure topologique, autrement dit l’organisation des ouverts dans un espace.

Et ainsi de suite.