Topologie des ensembles ouverts
Une topologie T sur un ensemble ouvert X désigne un ensemble de sous-ensembles de X considérés comme « ouverts » et doit répondre aux conditions suivantes :
- Par définition, l'ensemble vide Ø et l'ensemble X lui-même sont ouverts.
- L'union et l'intersection d'une quantité finie d'ensembles ouverts sont aussi considérées comme ouvertes.
En d'autres termes, l'ensemble T ne doit inclure que des sous-ensembles de X jugés « ouverts » et doit être fermé sous les opérations d'union et d'intersection.
Lorsqu'on parle d'une collection d'ensembles, il s'agit d'un ensemble dont les éléments sont eux-mêmes des ensembles ou des sous-ensembles.
Dans ces contextes, l'ensemble X et la topologie T forment un espace topologique, souvent représenté par le couple (X,T).
Note : Pour faire simple, on dit souvent que X est un espace topologique. Cependant, il est important de se souvenir qu'un espace topologique est constitué de deux éléments : la topologie T (une collection de sous-ensembles) et l'ensemble X.
Pourquoi considère-t-on toujours l'ensemble vide comme un ensemble ouvert ?
Par convention, l'ensemble vide est toujours considéré comme ouvert dans tout espace topologique.
Exemple concret
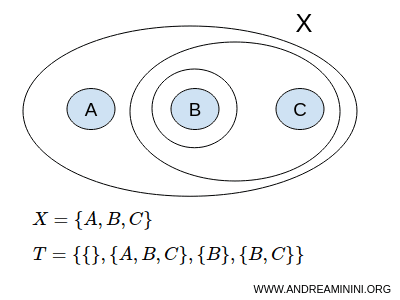
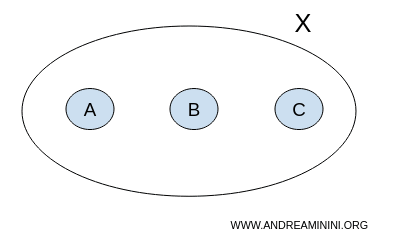
Considérons un ensemble X comprenant trois éléments : A, B et C
$$ X = \{ A,B,C \} $$
Une topologie T peut se définir comme l'ensemble des sous-ensembles suivants : { }, {A,B,C}, {B}, {B,C}.
$$ T = \{ \{ \},\{A,B,C\}, \{B\}, \{B,C\} \} $$
Le symbole { } désigne l'ensemble vide Ø, tandis que {A,B,C} représente l'ensemble lui-même, soit les sous-ensembles impropres de l'ensemble X.
Par définition, l'ensemble vide et l'ensemble complet X sont considérés comme des ensembles ouverts.
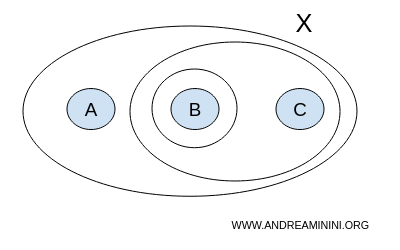
Une topologie est constituée d'ensembles ouverts. Ainsi, l'union et l'intersection d'ensembles ouverts doivent former un autre ensemble ouvert.
Dans notre cas, l'union des sous-ensembles de T appartient toujours à T, ce qui montre que T est stable par union.
$$ \{ B \} \cup \{ B, C \} \subseteq \{ B, C \} \subseteq T$$
$$ \{ B \} \cup \{ A, B, C \} \subseteq \{ A, B, C \} \subseteq T$$
$$ \{ B \} \cup \{ \} \subseteq \{ B \} \subseteq T $$
$$ \{ B \} \cup \{ B \} \subseteq \{ B \} \subseteq T$$
De même, l'intersection des sous-ensembles de T reste incluse dans T, confirmant que T est également stable par intersection.
$$ \{ B \} \cap \{ B, C \} \subseteq \{ B \} \subseteq T$$
$$ \{ B \} \cap \{ A, B, C \} \subseteq \{ B \} \subseteq T$$
$$ \{ B \} \cap \{ \} \subseteq \{ \} \subseteq T $$
$$ \{ B \} \cap \{ B \} \subseteq \{ B \} \subseteq T$$
Ainsi, l'ensemble T constitue une topologie sur X, remplissant toutes les conditions requises.
Exemple 2
Examinons un ensemble légèrement différent de celui de l'exemple précédent.
L'ensemble X demeure inchangé.
$$ X = \{ A,B,C \} $$
Toutefois, cette fois, la collection T s'enrichit du sous-ensemble {A}, venant s'ajouter aux sous-ensembles { }, {A,B,C}, {B} et {B,C}.
$$ T = \{ \{ \},\{A,B,C \}, \{ A \}, \{ B \}, \{ B,C \} \} $$
Ce nouvel assortiment de sous-ensembles n'est pas considéré comme une topologie de l'ensemble X, car il ne satisfait pas à toutes les conditions requises.
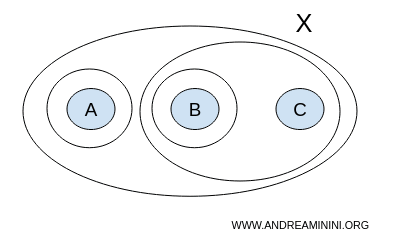
À titre d'exemple, l'union des sous-ensembles {A} et {B} forme un ensemble {A,B} qui ne figure pas dans la collection T.
$$\require{cancel} \{ A \} \cup \{ B \} = \{ A, B \} \cancel{\in} T $$
Ainsi, bien que les ensembles {A} et {B} soient considérés comme « ouverts » puisqu'ils appartiennent à la collection T, leur union ne résulte pas en un autre ensemble ouvert {A,B}, car cet ensemble n'est pas présent dans la collection.
$$ T = \{ \{ \},\{A,B,C \}, \{ A \}, \{ B \}, \{ B,C \} \} $$
Cela contrevient à l'une des conditions essentielles pour qu'une collection soit une topologie d'ensembles ouverts.
En conséquence, la collection T ne peut être considérée comme une topologie sur l'ensemble X.
Et ainsi de suite