Collections d’ensembles

Une collection d’ensembles est un ensemble dont les éléments sont eux-mêmes des ensembles.

Autrement dit, c’est un ensemble composé exclusivement d’ensembles.

Ce concept intervient dans de nombreux domaines des mathématiques, notamment en théorie des ensembles, en topologie et en algèbre abstraite.

À quoi cela sert-il ? Une collection d’ensembles permet de construire des structures mathématiques plus élaborées et d’étudier les relations entre différents ensembles.

Voici quelques exemples types de collections d’ensembles :

• Famille d’ensembles
  Il s’agit d’une collection d’ensembles partageant une propriété commune ou satisfaisant certains critères spécifiques. Un exemple classique est la famille de tous les ouverts d’un espace topologique.
• Partition d’un ensemble
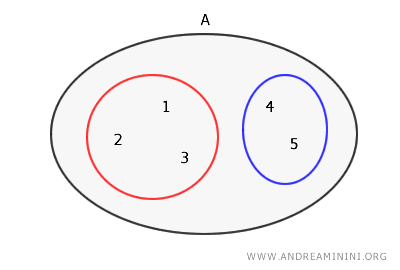
  Une partition d’un ensemble est une collection de sous-ensembles disjoints dont la réunion reconstitue exactement l’ensemble de départ. En d’autres termes, chaque élément appartient à un et un seul sous-ensemble de la partition.

  Par exemple, si l’on considère l’ensemble A = {1, 2, 3, 4, 5}, une partition possible de A est la collection formée par les sous-ensembles { {1, 2, 3}, {4, 5} }.
  

• Ensemble des parties (ensemble de tous les sous-ensembles)
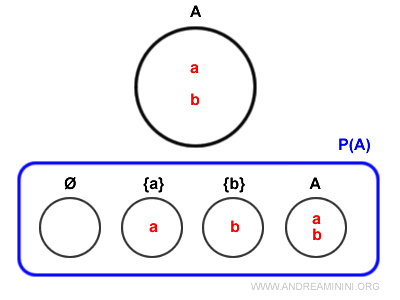
  Il s’agit de la collection constituée de tous les sous-ensembles possibles d’un ensemble donné, y compris l’ensemble vide et l’ensemble lui-même.

  Par exemple, pour l’ensemble A = {a, b}, son ensemble des parties P(A) est composé des sous-ensembles suivants : { {}, {a}, {b}, {a, b} }.
  

Ces notions jouent un rôle central dans l’analyse des structures mathématiques avancées et permettent d’explorer en profondeur les relations et propriétés des ensembles dans divers contextes théoriques.