Opérations sur les Ensembles

Les opérations sur les ensembles incluent l’union, l’intersection et la différence.

Pour illustrer clairement ces opérations, cette page s’appuie principalement sur des diagrammes de Venn, qui offrent une représentation visuelle plus intuitive que la seule notation mathématique.

Union

Étant donnés deux ensembles A et B, leur union est l’ensemble de tous les éléments qui appartiennent à A, à B, ou aux deux à la fois.

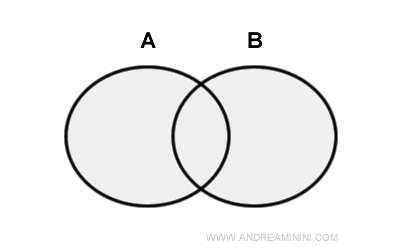
Le symbole utilisé pour désigner l’union est ∪.

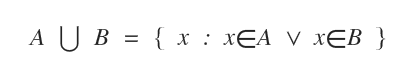
Dans une union, les éléments communs aux deux ensembles ne sont pris en compte qu’une seule fois.

Union d’une famille d’ensembles. L’union d’un ensemble d’ensembles s’écrit : $$ \bigcup_{i \in I} = \{ x \in A_i \:\: \text{pour un certain}\:\: i \in I \} $$

Comment déterminer l’union de deux ensembles

Voyons un exemple concret du calcul de l’union entre deux ensembles A et B.

Explication. L’ensemble A contient les éléments { 2, 5, 6, 7, 8 }, et l’ensemble B contient { 1, 3, 4, 6, 7, 9 }. Leur union donne : { 1, 2, 3, 4, 5, 6, 7, 8, 9 }. Les éléments communs {6, 7} ne sont répertoriés qu’une seule fois.

Intersection

L’intersection de deux ensembles A et B est l’ensemble des éléments qu’ils ont en commun.

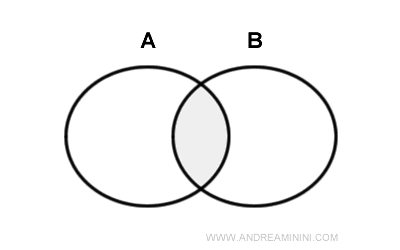
Le symbole de l’intersection est ⋂.

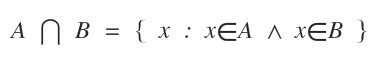
Deux ensembles A et B sont dits disjoints si leur intersection A⋂B est vide.

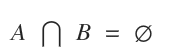
Intersection d’une famille d’ensembles. L’intersection d’une collection d’ensembles se note : $$ \bigcap_{i \in I} = \{ x \in A_i \:\: \forall i \in I \} $$

Comment déterminer l’intersection de deux ensembles

Voici un exemple concret d’intersection.

Explication. Les éléments { 6, 7 } figurent dans les deux ensembles, donc l’intersection A⋂B est { 6, 7 }.

Différence entre ensembles

La différence entre deux ensembles A et B, notée A - B, est l’ensemble des éléments qui appartiennent à A mais pas à B.

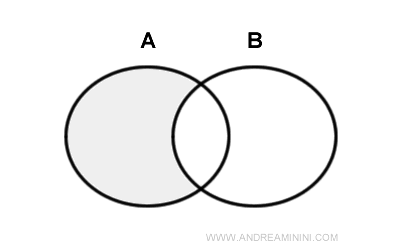
On l’appelle aussi complément de B dans A.

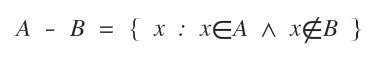
Remarque. La différence A - B, également appelée complément relatif de A par rapport à B, regroupe tous les éléments de A qui n’appartiennent pas à B. Elle se note : $$ A \text{ \ } B = \{ x \in A \mid x \notin B \} $$

Comment déterminer la différence entre deux ensembles

Exemple concret du calcul de la différence A - B.

Explication. L’ensemble A contient les éléments {2, 5, 6, 7, 8}. Les éléments {6, 7} étant communs aux deux ensembles, ils sont exclus de la différence. On obtient donc : {2, 5, 8}.

Propriétés des opérations sur les ensembles

Les opérations ensemblistes obéissent à plusieurs propriétés fondamentales : commutativité, associativité, distributivité et lois de De Morgan.

• Commutativité

  A ∪ B = B ∪ A
  A ∩ B = B ∩ A

• Associativité

  A ∪ (B ∪ C) = (A ∪ B) ∪ C
  A ∩ (B ∩ C) = (A ∩ B) ∩ C

• Distributivité

  A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C)
  A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)

• Lois de De Morgan

  A - (B ∪ C) = (A - B) ∩ (A - C)
  A - (B ∩ C) = (A - B) ∪ (A - C)