Borne inférieure et borne supérieure d’un ensemble

Que désigne-t-on par borne

Tout sous-ensemble non vide des nombres réels possède une borne inférieure et une borne supérieure, qui peuvent être finies ou infinies.

• Pour les ensembles bornés, ces deux bornes sont des nombres réels finis.
• Pour les ensembles non bornés, les bornes sont exprimées à l’aide des symboles plus ou moins l’infini (±∞).

Un ensemble peut être borné uniquement d’un côté. Il peut, par exemple, admettre une borne supérieure finie sans être borné inférieurement, ou inversement.

Remarque. Une borne peut appartenir à l’ensemble considéré, mais ce n’est pas toujours le cas.

Pour bien comprendre ces notions fondamentales, il est préférable d’étudier séparément la borne inférieure et la borne supérieure, à l’aide d’exemples concrets.

Borne inférieure (infimum)

Soit \( A \subseteq \mathbb{R} \) un ensemble et soit B un sous-ensemble non vide $$ B \subseteq A $$ La borne inférieure, ou infimum, de B est le nombre réel \( a \) tel que $$ a \le b \:\:\: \forall \, b \in B $$ et tel que tout nombre réel strictement supérieur à \( a \) ne soit plus une borne inférieure de B. $$ inf(B) = a $$

Autrement dit, l’infimum est la plus grande de toutes les bornes inférieures de l’ensemble B.

L’infimum peut appartenir ou non à l’ensemble. Lorsqu’il appartient à l’ensemble, on parle alors de minimum.

Par exemple, la borne inférieure de B est le nombre 3.

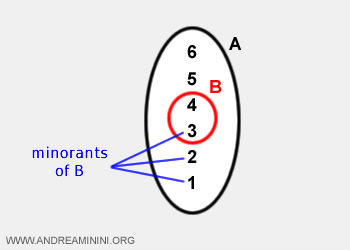
Dans un ensemble borné, la borne inférieure est un nombre réel fini. Elle correspond au maximum de l’ensemble de toutes les bornes inférieures (minorants).

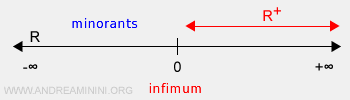
Si un ensemble n’est pas borné inférieurement, sa borne inférieure est définie comme moins l’infini (-∞).

Exemple 1

Soit A l’ensemble de tous les nombres réels \( \mathbb{R} \).

Soit B le sous-ensemble suivant :

$$ B = \{ 3, 4, 7, 5, 8, 9, 6 \} $$

La borne inférieure de B est 3.

$$ inf(B) = 3 \le b \:\:\: \forall \, b \in B $$

En effet, 3 est inférieur ou égal à tous les éléments de B.

Remarque. Ici, l’infimum appartient à l’ensemble, mais ce n’est pas toujours le cas.

Exemple 2

Soit B l’ensemble des nombres réels positifs \( \mathbb{R}^+ \).

La borne inférieure de B est 0.

$$ inf(B) \le b \:\:\: \forall \, b \in B $$

Ce nombre est la plus grande borne inférieure possible de \( \mathbb{R}^+ \).

Remarque. Dans ce cas, 0 n’appartient pas à l’ensemble B, car entre 0 et tout nombre réel positif, il existe une infinité de valeurs intermédiaires.

Borne supérieure (supremum)

Soit \( A \subseteq \mathbb{R} \) un ensemble et soit B un sous-ensemble non vide $$ B \subseteq A $$ La borne supérieure, ou supremum, de B est le nombre réel \( a \) tel que $$ a \ge b \:\:\: \forall \, b \in B $$ et tel que tout nombre réel strictement inférieur à \( a \) ne soit plus une borne supérieure de B. $$ sup(B) = a $$

De façon équivalente, le supremum est la plus petite de toutes les bornes supérieures de l’ensemble B.

Comme pour l’infimum, le supremum peut appartenir ou non à l’ensemble. Lorsqu’il appartient à l’ensemble, on parle de maximum.

Par exemple, la borne supérieure de B est 4.

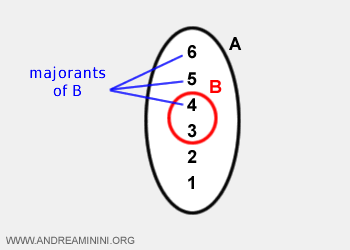
Dans un ensemble borné, la borne supérieure est un nombre réel fini. Elle correspond au minimum de l’ensemble des bornes supérieures (majorants).

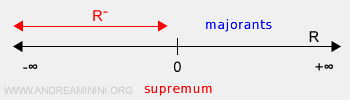
Si un ensemble n’est pas borné supérieurement, sa borne supérieure est définie comme plus l’infini (+∞).

Exemple 1

Soit B l’ensemble suivant :

$$ B = \{ 3, 4, 7, 5, 8, 9, 6 \} $$

La borne supérieure de B est 9.

$$ sup(B) = 9 \ge b \:\:\: \forall \, b \in B $$

Ce nombre est supérieur ou égal à tous les éléments de l’ensemble.

Remarque. Ici encore, la borne supérieure appartient à l’ensemble, mais ce n’est pas une règle générale.

Exemple 2

Soit B l’ensemble des nombres réels négatifs \( \mathbb{R}^- \).

La borne inférieure de B est moins l’infini.

$$ inf(B) = -\infty \le b \:\:\: \forall \, b \in B $$

Remarque. Dans ce cas, la borne inférieure appartient à la droite réelle étendue, mais pas à l’ensemble B, qui n’est pas borné inférieurement. En revanche, la borne supérieure \( sup(B)=0 \) n’appartient pas à l’ensemble, car 0 n’est pas un nombre réel négatif.

Caractérisations utiles en analyse

En analyse mathématique, il est souvent pratique de définir les bornes à l’aide de propriétés équivalentes, basées sur la notion de voisinage.

Borne inférieure d’un ensemble réel

Soit \( E \subset \mathbb{R} \) un ensemble borné inférieurement. Sa borne inférieure est le nombre réel \( m \) tel que :

• tout élément \( x \in E \) vérifie \( x \ge m \) ;
• pour tout \( \varepsilon > 0 \), il existe un élément \( x \in E \) tel que \( x < m + \varepsilon \).

On écrit alors \( m = \inf E \).

Cette définition exprime que \( m \) est la meilleure approximation possible par le bas des éléments de \( E \).

Borne supérieure d’un ensemble réel

Soit \( E \subset \mathbb{R} \) un ensemble borné supérieurement. Sa borne supérieure est le nombre réel \( M \) tel que :

• tout élément \( x \in E \) vérifie \( x \le M \) ;
• pour tout \( \varepsilon > 0 \), il existe un élément \( x \in E \) tel que \( x > M - \varepsilon \).

On écrit alors \( M = \sup E \).

Cette formulation souligne que \( M \) est la meilleure borne possible par le haut.

Notes finales

Quelques points essentiels à retenir

• Tout sous-ensemble non vide de \( \mathbb{R} \) admet une borne inférieure et une borne supérieure
  Si un ensemble n’est pas borné supérieurement, on définit sa borne supérieure par \( \sup A = +\infty \). De même, s’il n’est pas borné inférieurement, on pose \( \inf A = -\infty \). Lorsqu’un ensemble est borné, ses bornes finies existent et sont uniques. Les notions de borne inférieure et supérieure sont ainsi toujours bien définies dans le cadre des nombres réels étendus.

  On appelle nombres réels étendus l’ensemble obtenu en complétant la droite réelle \( \mathbb{R} \) par les symboles \( -\infty \) et \( +\infty \). Ces symboles ne sont pas des nombres réels, mais ils permettent de donner un sens général aux notions de borne.

Et ainsi de suite.