Différence entre Ensembles

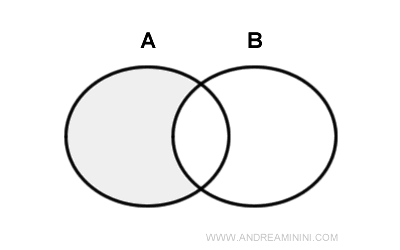
La différence entre deux ensembles A et B est l’ensemble (appelé ensemble différence) formé des éléments de A qui n’appartiennent pas à B. $$ A - B = \{ x \ | \ x \in A \ \land \ x \notin B \} $$ On lit cette expression : « A moins B ». Le diagramme de Venn ci-dessous illustre cette opération :

Dans certains cas, la différence peut également être notée :

$$ A \text{ \ } B $$

Ce qui se lit : « le complément de B dans A ».

Exemple concret

Soient deux ensembles finis A et B :

$$ A = \{ 0, 2, 4, 8, 10 \} $$

$$ B = \{ 2, 4, 6, 12 \} $$

La différence A - B correspond aux éléments de A qui ne figurent pas dans B :

$$ A - B = A \text{ \ } B = \{ 0, 8, 10 \} $$

L’ensemble différence est donc constitué des éléments {0, 8, 10}.

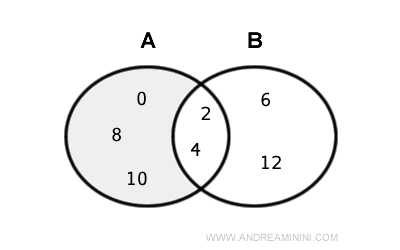
Les éléments communs à A et B - ici 2 et 4 - sont exclus de la différence.

Exemple 2

Considérons maintenant un autre cas avec les ensembles suivants :

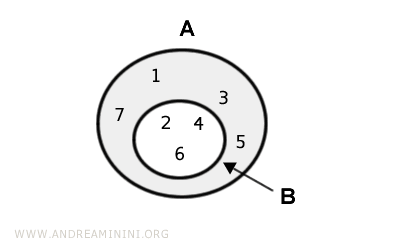
$$ A = \{ 1, 2, 3, 4, 5, 6, 7 \} $$

$$ B = \{ 2, 4, 6 \} $$

Ici, B est un sous-ensemble propre de A.

La différence A - B contient les éléments de A qui ne sont pas dans B :

$$ A - B = A \text{ \ } B = \{ 1, 3, 5, 7 \} $$

L’ensemble différence est donc constitué des éléments {1, 3, 5, 7}.

Dans le diagramme d’Euler-Venn, cette région est représentée en gris :

Propriétés de la Différence

Voici quelques propriétés fondamentales de l’opération de différence :

• La différence n’est pas commutative $$ A - B \ne B - A $$

  Exemple : Soient $$ A = \{ 0, 2, 4, 8, 10 \} $$ et $$ B = \{ 2, 4, 6, 12 \} $$
  On a : $$ A - B = \{ 0, 8, 10 \} $$
  tandis que : $$ B - A = \{ 6, 12 \} $$

• Si A et B sont disjoints, alors A - B = A $$ A \cap B = \emptyset \Longleftrightarrow A - B = A $$

  Exemple : Soient $$ A = \{ 2, 4, 6, 8 \} $$ et $$ B = \{ 1, 3, 5, 7, 9 \} $$.
  Ces ensembles étant disjoints, leur intersection est vide, et donc : $$ A - B = A = \{ 2, 4, 6, 8 \} $$
  Représentation graphique :
  
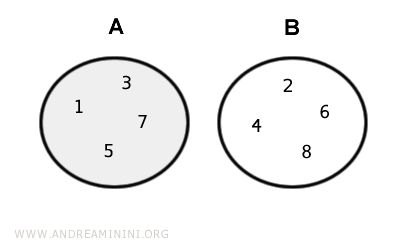
  De même : $$ B - A = B = \{ 1, 3, 5, 7, 9 \} $$

• Si A et B sont identiques, alors A - B est l’ensemble vide $$ A = B \Longleftrightarrow A - B = \Oslash $$

Ces propriétés sont valables pour tout couple d’ensembles et facilitent le raisonnement dans les opérations ensemblistes.