Théorie des Ensembles
La théorie des ensembles repose sur l’utilisation du concept d’ensemble au sein du langage logico-mathématique.
Définition d’un Ensemble
Un ensemble est une collection d’objets, appelés éléments ou membres, partageant une propriété spécifique. On peut également le désigner par les termes classe, ensemble ou famille.
Ce concept est fondamental car il ne peut pas être défini à partir d’autres notions plus élémentaires.
Dans un ensemble, l’ordre des éléments est sans importance.
Définition d’un Ensemble en Mathématiques
En mathématiques, un ensemble est un groupe d’objets pour lequel il existe un critère objectif permettant de déterminer si un objet donné appartient ou non à ce groupe.
Lorsqu’on parle d’un ensemble mathématique, on fait référence à un ensemble bien défini dans lequel tous les objets satisfont un critère objectif d’appartenance.
En revanche, les ensembles définis sur la base de critères subjectifs ne sont pas considérés comme des ensembles mathématiques.
Désormais, lorsque j’évoquerai le mot « ensemble », il s’agira d’ensembles au sens mathématique.
Exemple. L’ensemble des nombres premiers est un ensemble mathématique, car le critère d’appartenance est objectif. Il comprend tous les nombres naturels divisibles uniquement par 1 et par eux-mêmes. $$ I = \{ 2 , 3, 5, 7, 11, ... \} $$ À l’inverse, l’ensemble des meilleures chansons n’est pas un ensemble mathématique, car le critère d’appartenance est subjectif et varie d’une personne à l’autre.
Représentation des Ensembles
Dans le langage logico-mathématique, les ensembles sont désignés par des lettres majuscules (A, B, C, D, ...).
Les éléments d’un ensemble, quant à eux, sont généralement notés avec des lettres minuscules (a, b, c, d, ...).
Symboles d’Appartenance et de Non-Appartenance
Le symbole indiquant qu’un élément appartient à un ensemble est ∈.
On le lit « l’élément x appartient à l’ensemble A ».
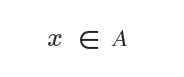
Le symbole indiquant qu’un élément n’appartient pas à un ensemble est ∉.
Il se lit « l’élément x n’appartient PAS à l’ensemble A ».
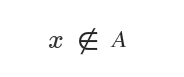
Exemple. Considérons l’ensemble B des nombres pairs compris entre 1 et 9. $$ B = \{ \ 2 \ , \ 4 \ , \ 6 \ , \ 8 \ \} $$ Pour indiquer que le nombre 2 appartient à l’ensemble B, on écrit $$ 2 \in B $$ Pour indiquer que le nombre 3 n’appartient PAS à l’ensemble B, on écrit $$ 3 \notin B $$
Représentation Graphique
Pour représenter graphiquement un ensemble, on utilise des diagrammes d’Euler-Venn, également appelés cercles d’Euler.
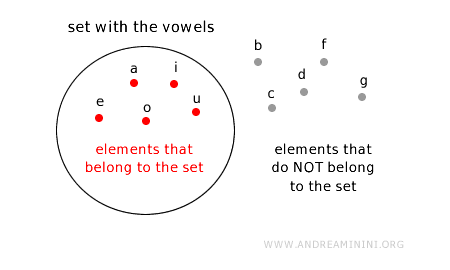
Chaque ensemble est représenté par un cercle, une ellipse ou une figure fermée.
Les éléments appartenant à l’ensemble sont placés à l’intérieur de la figure.
Les éléments qui n’appartiennent pas à l’ensemble se trouvent à l’extérieur.
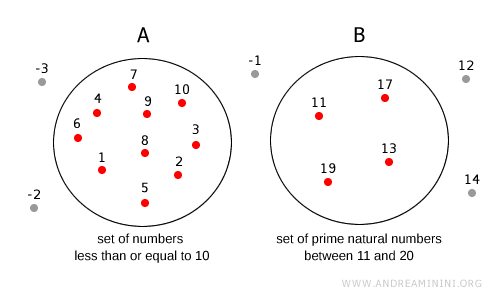
Remarque. L’ensemble A contient les nombres naturels jusqu’à 10. Tous les nombres situés hors du cercle A n’appartiennent pas à A. Dans l’ensemble B, en revanche, figurent les nombres premiers compris entre 11 et 20. De même, tous les nombres en dehors du cercle B ne font pas partie de B. Les nombres en dehors des deux cercles (-1, -2, -3, 12, 14, ...) n’appartiennent ni à A ni à B.
Si un élément appartient à deux ensembles, il doit se trouver à l’intersection des deux figures.
Par exemple, si l’ensemble B correspondait à l’ensemble des nombres premiers compris entre 1 et 20, il faudrait représenter A et B comme deux ensembles qui se chevauchent.

Dans ce cas, les éléments communs aux deux ensembles A⋂B={1, 2, 3, 5, 7} figurent simultanément dans A et dans B.
Remarque. Les diagrammes d’Euler-Venn doivent leur nom au mathématicien suisse Leonhard Euler et au mathématicien anglais John Venn, qui furent parmi les premiers à les utiliser pour représenter des ensembles.
Représentation Tabulaire ou Énumérative
Un ensemble simple peut également être représenté sous forme tabulaire.
Dans la représentation tabulaire, les éléments de l’ensemble sont inscrits entre accolades et séparés par des virgules.
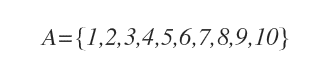
Cette forme est également appelée notation énumérative.
Il n’est pas nécessaire d’énumérer les éléments dans un ordre particulier. L’ordre est sans importance.
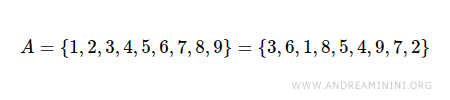
Tout élément répété dans un ensemble ne doit apparaître qu’une seule fois en notation énumérative.
Il ne doit donc pas y avoir de doublons à l’intérieur des accolades.
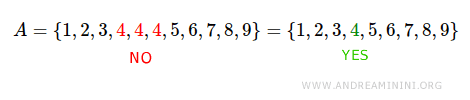
La représentation tabulaire est pratique lorsqu’un ensemble est fini et comporte peu d’éléments.
Elle devient fastidieuse si l’ensemble contient un grand nombre d’éléments.
Remarque. On utilise parfois des points de suspension ... lorsque la règle d’appartenance à l’ensemble est suffisamment explicite, et que les éléments non listés sont sous-entendus. Par exemple, A={1,2,...,10} désigne l’ensemble des nombres naturels de 1 à 10. $$ A = \{ \ 1,2, \ ... \ ,10 \ \} $$ Dans la notation tabulaire, les points de suspension ... peuvent également indiquer un ensemble infini. Par exemple, A={1,2,3,...} désigne l’ensemble de tous les nombres naturels à partir de 1. $$ A=\{ \ 1,2,3 \ ... \ \} $$
Notation en Compréhension
Un ensemble peut également être défini au moyen de la notation en compréhension, qui repose sur la règle ou la propriété caractéristique des éléments de l’ensemble.
Cette notation est particulièrement utile lorsqu’un ensemble contient de nombreux éléments ou lorsqu’il est infini.
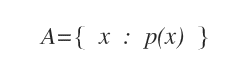
À l’intérieur des accolades, la règle d’appartenance à l’ensemble, également appelée propriété caractéristique, est exprimée à l’aide du langage formel de la logique mathématique.
Exemple. En notation en compréhension, l’ensemble des nombres naturels de 1 à 10 se note A={x∈N:0
Avantages et Inconvénients des Notations
La notation en compréhension permet de représenter tout type d’ensemble, fini ou infini, dès lors que les éléments peuvent être définis par un ou plusieurs critères précis.
La notation énumérative, en revanche, n’est utilisable que si :
- l’ensemble est fini et comporte peu d’éléments
- l’ensemble est fini ou infini et peut être représenté en indiquant seulement quelques éléments, les autres étant sous-entendus.
Enfin, la représentation graphique est particulièrement précieuse pour illustrer ou transmettre visuellement des concepts qui, autrement, seraient difficiles à appréhender avec la seule notation logico-mathématique.
Ensembles Finis et Infinis
Un ensemble peut être fini ou infini.
- Un ensemble fini contient un nombre fini n d’éléments.
Exemple. L’ensemble des livres dans un sac à dos est un ensemble fini. Un autre exemple est l’ensemble des grains de sable dans un récipient.
- Un ensemble infini contient une infinité d’éléments.
Exemple. L’ensemble des nombres naturels est infini, car à chaque nombre naturel (n) correspond un successeur (n+1). Il n’existe pas de nombre naturel qui soit supérieur à tous les autres.
Ensembles Numériques
Les ensembles numériques sont des ensembles constitués de nombres.
Par convention, en mathématiques, on désigne ces ensembles à l’aide de lettres majuscules spécifiques.
- N désigne l’ensemble des nombres naturels
- Z désigne l’ensemble des nombres entiers
- Q désigne l’ensemble des nombres rationnels
- I désigne l’ensemble des nombres irrationnels
- R désigne l’ensemble des nombres réels
- C désigne l’ensemble des nombres complexes
L’Ensemble Vide
L’ensemble vide est un ensemble sans éléments. Il est représenté par le symbole Ø. $$ Ø = \{ \ \ \} $$
On le note parfois par deux accolades vides.
C’est un ensemble particulier, car l’ensemble vide est un sous-ensemble de tout autre ensemble.
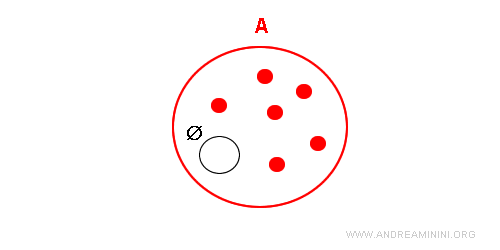
Il n’existe qu’un seul ensemble vide. Par exemple, l’ensemble des nombres naturels impairs divisibles par deux est vide, car aucun nombre naturel impair n’est divisible par deux. De même, l’ensemble des carrés à trois côtés est vide, puisqu’un carré possède toujours quatre côtés. Dans les deux cas, il s’agit du même ensemble vide, bien que les critères d’appartenance diffèrent.
Et ainsi de suite.