Bornes supérieure et inférieure

Comprendre les bornes supérieure et inférieure

Soient A un ensemble et B un sous-ensemble de A, noté B ⊆ A.

• Un élément \( k \in A \) est une borne inférieure (ou minorant) de B si \( k \le b \) pour tout \( b \in B \).

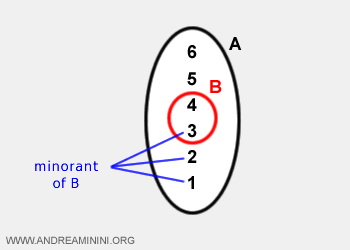
  Exemple : considérons A = {1, 2, 3, 4, 5, 6} et B = {3, 4}. Les bornes inférieures de B sont {1, 2, 3}.
  

• Un élément \( k \in A \) est une borne supérieure (ou majorant) de B si \( k \ge b \) pour tout \( b \in B \).

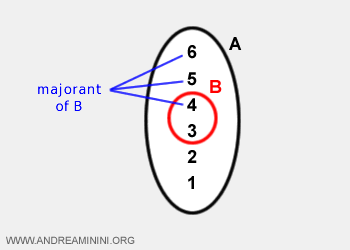
  Exemple : avec les mêmes ensembles A et B, les bornes supérieures de B sont {4, 5, 6}.
  

Étendue des bornes dans un ensemble

Un ensemble peut admettre plusieurs bornes supérieures et inférieures, ou bien n’en admettre aucune.

Exemples illustratifs

Certains ensembles possèdent des bornes inférieures mais aucune borne supérieure : on les appelle ensembles majorés inférieurement.

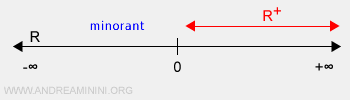
Exemple d’un ensemble sans borne supérieure : l’ensemble des réels positifs \( \mathbb{R}^+ \), défini comme l’intervalle ouvert (0, +∞), est un sous-ensemble infini de \( \mathbb{R} \). Il admet des bornes inférieures telles que zéro et tous les réels négatifs, bien que celles-ci n’appartiennent pas à \( \mathbb{R}^+ \) lui-même. Par exemple, zéro n’est pas un élément de \( \mathbb{R}^+ \), et entre zéro et tout réel strictement positif, on trouve une infinité de réels. En revanche, \( \mathbb{R}^+ \) n’est pas borné supérieurement, car il s’étend indéfiniment vers +∞.

D’autres ensembles, au contraire, disposent de bornes supérieures mais sont dépourvus de bornes inférieures : ce sont les ensembles majorés supérieurement.

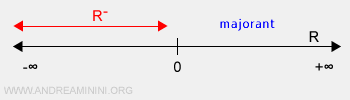
Exemple d’un ensemble sans borne inférieure : l’ensemble des réels négatifs \( \mathbb{R}^- \), soit l’intervalle ouvert (-∞, 0), est un sous-ensemble infini de \( \mathbb{R} \). Il admet des bornes supérieures telles que zéro et tous les réels positifs, bien que ces éléments ne fassent pas partie de \( \mathbb{R}^- \). Par exemple, zéro n’appartient pas à \( \mathbb{R}^- \), et il existe une infinité de réels entre tout réel négatif et zéro. En revanche, \( \mathbb{R}^- \) n’a aucune borne inférieure, car il s’étend sans fin vers -∞.

Il existe également des ensembles qui sont à la fois bornés inférieurement et supérieurement : on les appelle ensembles bornés.

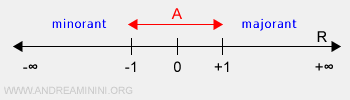
Exemple d’un ensemble borné : l’ensemble des réels compris entre -1 et +1 est un sous-ensemble de \( \mathbb{R} \). Il possède une infinité de bornes inférieures situées dans l’intervalle (-∞, -1), et une infinité de bornes supérieures dans l’intervalle (1, +∞).

Enfin, certains ensembles ne possèdent ni borne supérieure ni borne inférieure.

Exemple d’un ensemble sans bornes : l’ensemble vide est un sous-ensemble impropre de tout ensemble universel. Par définition, il ne possède ni borne inférieure ni borne supérieure. De même, un ensemble non borné tel que \( \mathbb{R} \) - l’ensemble des réels tout entier - est improprement inclus en lui-même et n’admet donc aucune borne.

Et ainsi de suite.