Sous-ensembles Propres
Qu’est-ce qu’un sous-ensemble propre ?
- On dit qu’un ensemble A est un sous-ensemble propre d’un ensemble B lorsque :
- tous les éléments de A appartiennent également à B,
- mais B contient au moins un élément qui n’appartient pas à A.
Cette relation est appelée inclusion stricte.
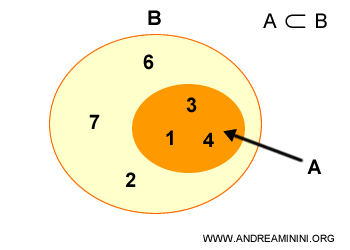
Il s’agit d’un cas particulier d’inclusion, noté à l’aide du symbole ⊂.
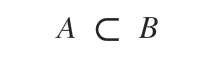
Cette notation se lit : « l’ensemble A est une partie propre de l’ensemble B » ou « l’ensemble A est strictement inclus dans l’ensemble B ».
L’inclusion stricte implique que les deux ensembles sont distincts, autrement dit, A≠B.
Quelle est la différence entre inclusion ordinaire et inclusion stricte ? Une inclusion stricte (A⊂B) suppose nécessairement que A et B ne sont pas égaux (A≠B), car B possède au moins un élément absent de A. En revanche, une inclusion ordinaire (A⊆B) permet que les deux ensembles soient identiques (A=B). Ainsi, si A est strictement inclus dans B (A⊂B), cela entraîne aussi l’inclusion ordinaire (A⊆B). Mais l’inverse n’est pas toujours vrai : si A est inclus dans B au sens ordinaire (A⊆B), il se peut que les deux ensembles soient en réalité égaux, et donc que l’inclusion ne soit pas stricte.
Exemple
L’ensemble A contient trois éléments, tandis que l’ensemble B en compte six.
$$ A = \{ 1,3,4 \} $$
$$ B = \{ 1,3,4,2,6,7 \} $$
La première condition d’inclusion stricte est remplie, car tous les éléments de A figurent dans B.
$$ A = \{ 1,3,4 \} ⊂ B $$
La seconde condition est également satisfaite, puisque B contient des éléments supplémentaires absents de A.
Dans cet exemple, les éléments {2,6,7} appartiennent à B mais pas à A.
$$ B = \{ 1,3,4,\color{red}2,\color{red}6,\color{red}7 \} $$
On en conclut que A est strictement inclus dans B, autrement dit, A est un sous-ensemble propre de B.
$$ A ⊂ B $$
Et ainsi de suite.