Intersection d’Ensembles

L’intersection de deux ensembles A et B désigne l’ensemble de tous les éléments qui appartiennent simultanément à A et à B.

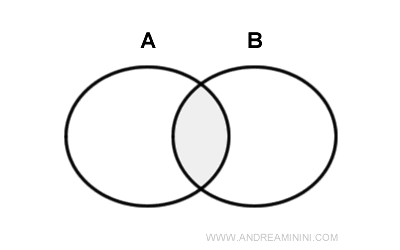
Le symbole utilisé pour l’intersection est ⋂.

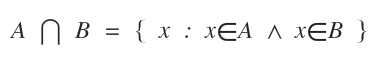
Cette notation se lit : « l’intersection de A et B » ou « A inter B ».

Intersection de plusieurs ensembles. Lorsqu’on considère l’intersection de plusieurs ensembles, on peut utiliser une notation abrégée : $$ \bigcap_{i \in I} = \{ x \in A_i \mid \forall i \in I \} $$

Lorsque deux ensembles n’ont aucun élément en commun, leur intersection est l’ensemble vide : $$ A \cap B = \Oslash $$

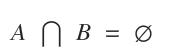
Dans ce cas, les ensembles A et B sont dits disjoints.

Exemple concret

Soient deux ensembles finis A et B :

$$ A = \{ 2, 5, 6, 7, 8 \} $$

$$ B = \{ 1, 3, 4, 6, 7, 9 \} $$

On constate que ces deux ensembles ont deux éléments en commun :

$$ A = \{ 2, 5, \color{red}6, \color{red}7, 8 \} $$

$$ B = \{ 1, 3, 4, \color{red}6, \color{red}7, 9 \} $$

L’intersection de A et B est donc :

$$ A \cap B = \{ 6, 7 \} $$

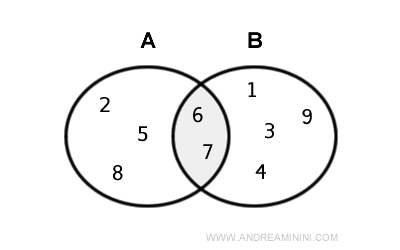
Voici sa représentation dans un diagramme d’Euler-Venn :

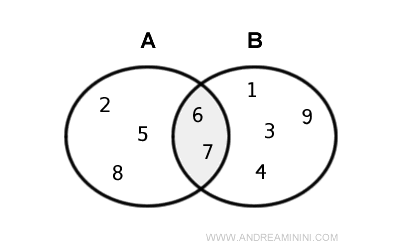
Types d’Intersection

Selon la relation entre les ensembles considérés, leur intersection peut prendre différentes formes :

• L’intersection \( A \cap B \) est un sous-ensemble propre des deux ensembles.

  Exemple. Soient $$ A = \{ 2, 5, 6, 7, 8 \} $$ et $$ B = \{ 1, 3, 4, 6, 7, 9 \} $$. Leur intersection est $$ A \cap B = \{ 6, 7 \} $$.
  Elle constitue un sous-ensemble propre à la fois de A et de B : $$ A \cap B ⊂ A \quad \text{et} \quad A \cap B ⊂ B $$
  Il s’agit de l’exemple illustré précédemment.
  

• L’intersection \( A \cap B \) est un sous-ensemble propre de l’un et un sous-ensemble impropre de l’autre. Cela se produit lorsque l’un des deux ensembles est entièrement inclus dans l’autre (par exemple, \( A \subseteq B \)).

  Exemple. Soient $$ A = \{ 3, 6, 7 \} $$ et $$ B = \{ 1, 3, 4, 6, 7, 9 \} $$.
  Leur intersection est $$ A \cap B = \{ 3, 6, 7 \} $$.
  Représentation graphique :
  
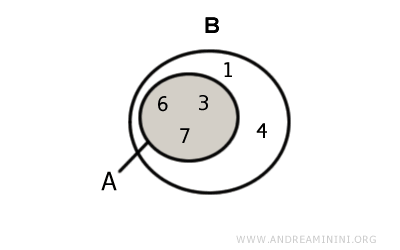
  Ici, l’intersection est égale à A, ce qui en fait un sous-ensemble impropre de A : $$ A \cap B = A $$
  Tandis qu’elle reste un sous-ensemble propre de B : $$ A \cap B ⊂ B $$

• L’intersection \( A \cap B \) est un sous-ensemble impropre des deux ensembles. Cela peut se produire dans deux cas :
  
  A] Lorsque les ensembles sont disjoints, leur intersection est l’ensemble vide, qui est un sous-ensemble impropre de tout ensemble.

  Exemple. Soient $$ A = \{ 2, 5, 8 \} $$ et $$ B = \{ 1, 3, 4, 6, 7, 9 \} $$.
  Comme ils n’ont aucun élément en commun : $$ A \cap B = \Oslash $$
  
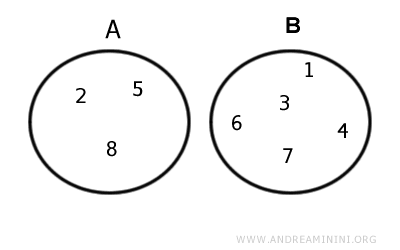
  L’ensemble vide est un sous-ensemble impropre de A et de B : $$ A \cap B ⊂ A \quad \text{et} \quad A \cap B ⊂ B $$

  B] Lorsque les ensembles sont identiques. Dans ce cas, leur intersection est égale à chacun d’eux :

  Exemple. Soient $$ A = \{ 1, 2, 3, 4 \} $$ et $$ B = \{ 1, 2, 3, 4 \} $$.
  On a alors : $$ A \cap B = A = B $$
  
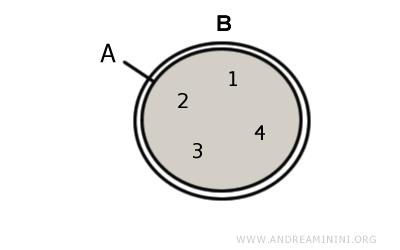
  Lorsque deux ensembles sont égaux, chacun est un sous-ensemble impropre de l’autre.

Propriétés de l’Intersection

L’opération d’intersection satisfait plusieurs propriétés fondamentales, analogues à celles de la multiplication :

• Commutativité
  L’ordre des ensembles n’affecte pas le résultat : $$ A \cap B = B \cap A $$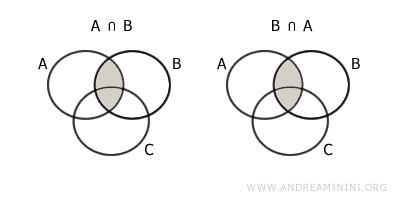

  

• Associativité
  $$ (A \cap B) \cap C = A \cap (B \cap C) $$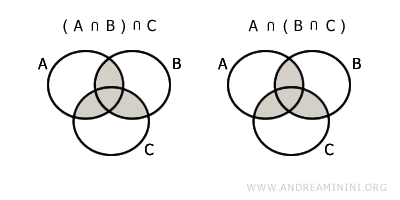

  

• Distributivité par rapport à l’union
  $$ A \cap (B \cup C) = (A \cap B) \cup (A \cap C) $$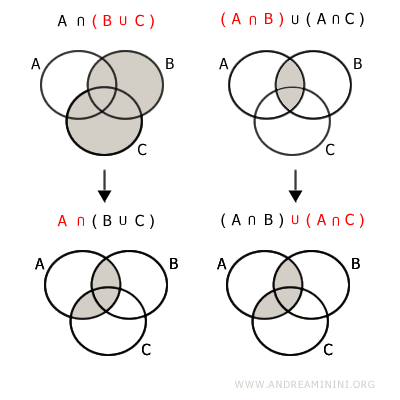

  

Et ainsi de suite.