Produit Cartésien

Le produit cartésien est une opération mathématique qui associe deux ensembles.

Définition

Étant donnés deux ensembles A et B, le produit cartésien A×B est l’ensemble de tous les couples ordonnés (a, b), où « a » appartient à A et « b » appartient à B.

En notation mathématique, le produit cartésien s’écrit :

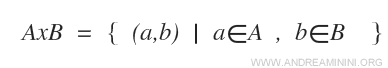
On le lit « A fois B » ou « produit cartésien de A par B ».

Un Exemple Concret

Pour mieux saisir ce concept, prenons un exemple simple.

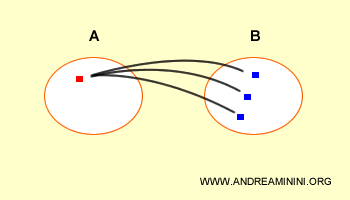
Soient deux ensembles A et B, le premier contenant deux éléments, le second trois.

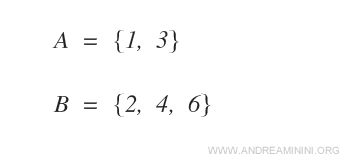
Le produit cartésien A×B est l’ensemble suivant :

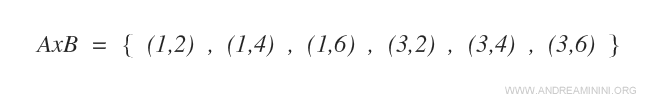
Chaque élément de A×B est un couple ordonné.

Visuellement, la correspondance entre les deux ensembles peut être représentée comme suit :

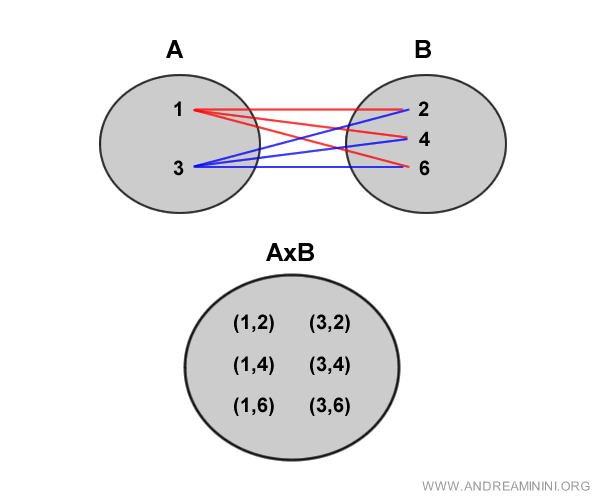
Remarque. Les éléments du produit cartésien ne sont pas des éléments isolés de A ou de B, mais des couples construits à partir de chacun d’eux.

Dans un repère cartésien, ces couples peuvent être interprétés comme des points de coordonnées (x, y).

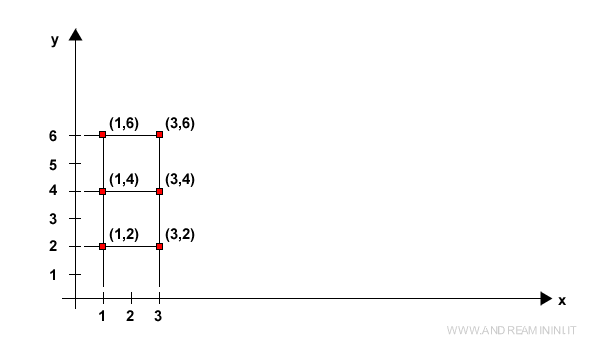
Comment Représenter un Produit Cartésien ?

Il existe plusieurs façons de représenter un produit cartésien :

• Diagramme cartésien
  On place les éléments de A sur l’axe horizontal (x) et ceux de B sur l’axe vertical (y). Chaque couple (a, b) correspond à un point unique de coordonnées (x = a, y = b).
  
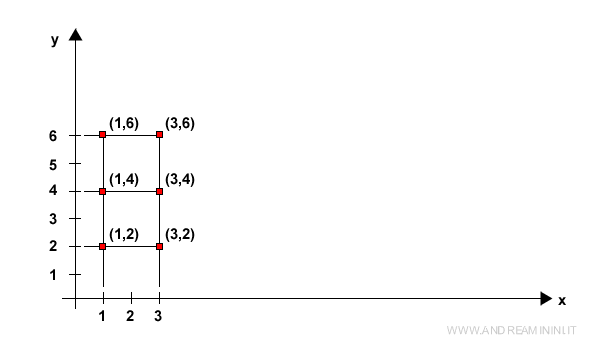
• Tableau à double entrée
  Les éléments de A sont disposés en ligne, ceux de B en colonne. Chaque case du tableau contient le couple associé à l’intersection ligne-colonne.
  

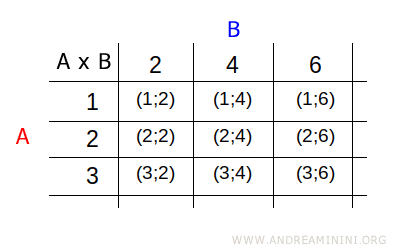
  Remarque. Cette représentation est particulièrement utile lorsque les ensembles ne contiennent pas uniquement des nombres.

Qu’est-ce Qu’un Couple Ordonné ?

Un couple ordonné (a, b) est une paire dans laquelle l’ordre des éléments est essentiel : « a » est le premier, « b » le second.

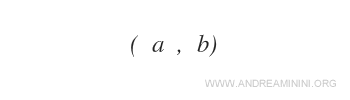
Il s’écrit entre parenthèses, avec les éléments séparés par une virgule.

Les deux éléments peuvent être identiques.

L’ordre est fondamental

Dans un couple ordonné, inverser les éléments donne un résultat différent.

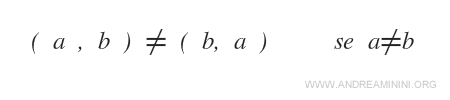
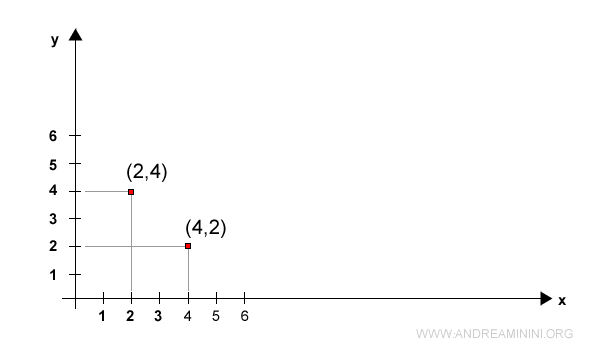
Exemple

Les couples (2, 4) et (4, 2) ne sont pas équivalents : bien qu’ils contiennent les mêmes nombres, leur ordre change leur signification.

Quand Deux Couples Ordonnés Sont-Ils Égaux ?

Deux couples (a, b) et (c, d) sont égaux si et seulement si a = c et b = d, c’est-à-dire si leurs éléments correspondent exactement dans le même ordre.

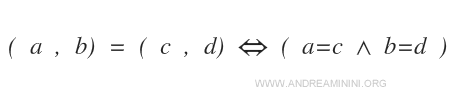
Le Produit Cartésien Est-Il Commutatif ?

Le produit cartésien n’est pas commutatif.

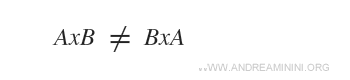
Exemple

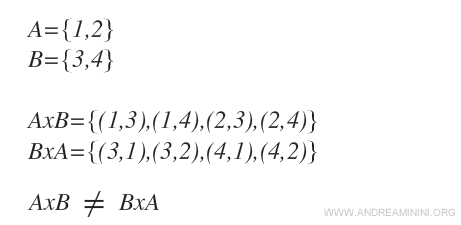
On voit clairement que A×B ≠ B×A, car l’ordre des éléments dans un couple est significatif.

Cette différence devient encore plus visible lorsqu’on représente les deux produits dans le plan.

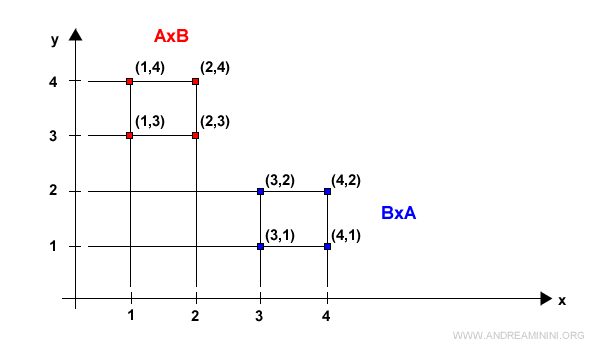
Remarque. Le seul cas où A×B = B×A est celui où A = B. Si les deux ensembles sont identiques, le produit cartésien devient alors symétrique.

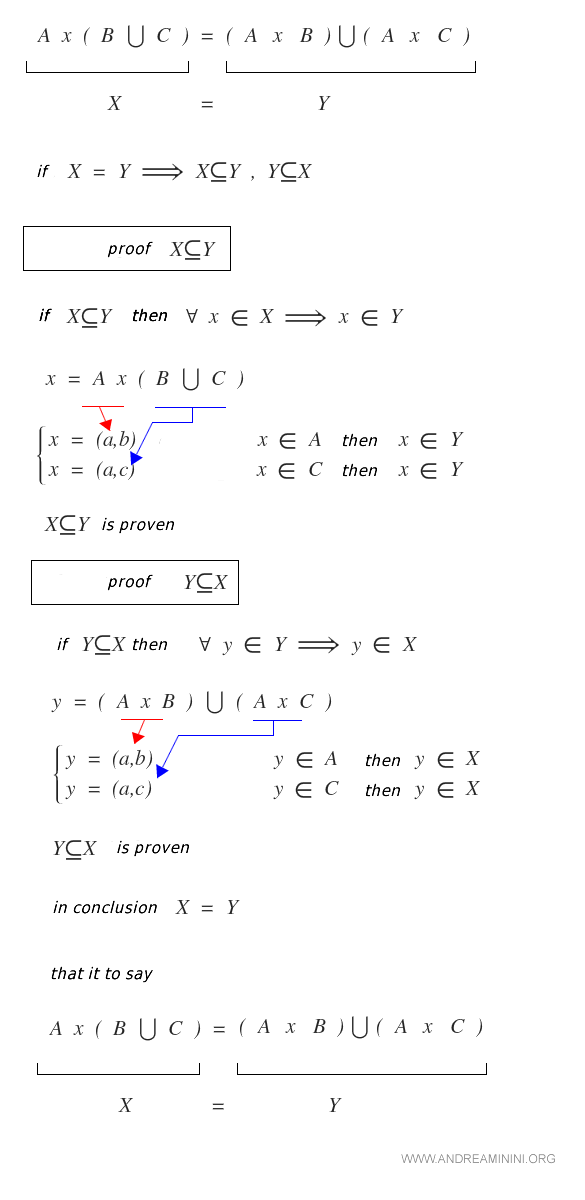
Propriété Distributive

Le produit cartésien est distributif par rapport à l’union et à l’intersection d’ensembles.

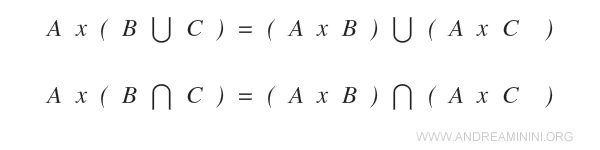
Démonstration

Produit Cartésien avec un Ensemble Vide

Si l’un des deux ensembles est vide, alors leur produit cartésien est également vide.

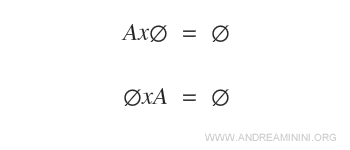
Produit Cartésien de n Ensembles

Le produit cartésien peut être généralisé à un nombre quelconque n d’ensembles.

Étant donnés n ensembles A₁, A₂,..., A_n, leur produit cartésien A₁×A₂×...×A_n est l’ensemble de toutes les n-uplets (a₁, a₂,..., a_n) telles que : $$ A_1 \times A_2 \times \dots \times A_n = \{ (a_1, a_2, ..., a_n) \mid a_i \in A_i,\ i = 1, 2, ..., n \} $$

Chaque élément a_i appartient à l’ensemble A_i correspondant.

Produit Cartésien d’un Ensemble avec Lui-Même

On peut également former le produit cartésien d’un ensemble avec lui-même.

Exemple

Soit l’ensemble A :

$$ A = \{ 1, 2, 3 \} $$

Son produit cartésien avec lui-même, A×A, est donné par :

$$ A \times A = \{ (1,1), (1,2), (1,3), (2,1), (2,2), (2,3), (3,1), (3,2), (3,3) \} $$

Ce principe peut être étendu à des produits de dimension supérieure, produisant des triplets, quadruplets ou n-uplets.