Ensemble Vide

L’ensemble vide est un ensemble qui ne contient aucun élément. On le note à l’aide du symbole Ø ou bien par une paire d’accolades vides { }.

Le symbole de l’ensemble vide, ∅, se lit « ensemble vide » ou tout simplement « vide ».

Un Exemple Concret d’Ensemble Vide

L’ensemble des nombres naturels impairs divisibles par deux est vide, car aucun nombre impair ne peut être divisible par deux.

Il n’existe qu’un seul ensemble vide. L’ensemble des nombres naturels impairs divisibles par deux est vide. De même, l’ensemble des triangles ayant quatre côtés est également vide. Dans les deux cas, bien que les conditions de définition soient différentes, il s’agit toujours du même ensemble vide. $$ Ø = \{ \ \ \} $$

La notion d’ensemble vide soulève des questions fascinantes sur la nature de l’existence en mathématiques, puisqu’il s’agit d’un objet qui, bien qu’il ne contienne rien, possède néanmoins une existence propre.

On pourrait le décrire comme le « néant » qui, paradoxalement, est « quelque chose » dans l’univers mathématique.

L’Ensemble Vide comme Sous-ensemble Impropre

L’ensemble vide est considéré comme un sous-ensemble impropre de tout ensemble.

Démonstration

Pour le démontrer, on raisonne par l’absurde.

Soit A un ensemble quelconque. Supposons, pour parvenir à une contradiction, que l’ensemble vide ne soit pas un sous-ensemble de A.

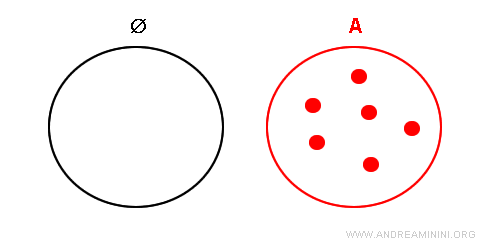
Cette hypothèse impliquerait qu’il existe au moins un élément dans l’ensemble vide qui ne se trouve pas dans A.

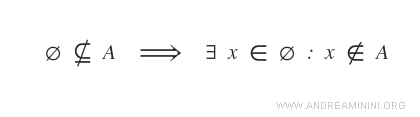
Or, cela est impossible puisque l’ensemble vide ne contient aucun élément.

Face à cette contradiction, il faut conclure que la supposition initiale est fausse : l’ensemble vide est bien un sous-ensemble de A.

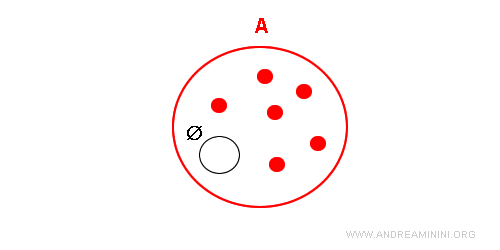
C’est pour cette raison que l’ensemble vide est reconnu comme un sous-ensemble impropre de tout ensemble.

Autre Démonstration. L’union d’un ensemble A avec l’un quelconque de ses sous-ensembles B ⊆ A est toujours égale à A lui-même : $$ A \cup B = A $$ En particulier, si l’on prend B comme l’ensemble vide, on obtient : $$ A \cup Ø = A $$ Ce qui prouve que l’ensemble vide est bien un sous-ensemble de A.

Propriétés Essentielles de l’Ensemble Vide

• L’ensemble vide est unique
  En mathématiques, il n’existe qu’un seul ensemble vide. Quel que soit le contexte dans lequel il est évoqué, il s’agit toujours du même objet mathématique.

  Cette unicité est fondamentale, car elle assure que toutes les propriétés liées à l’ensemble vide sont universelles et indépendantes du contexte ou de la notation. C’est pourquoi on parle toujours de « l’ensemble vide » au singulier et non de « les ensembles vides ».

• Il est sous-ensemble de tout ensemble
  Il est considéré comme un sous-ensemble impropre de tout autre ensemble.

  Rappelons la définition d’un sous-ensemble : un ensemble \(A\) est sous-ensemble d’un ensemble \(B\) si chaque élément de \(A\) appartient également à \(B\). Comme l’ensemble vide, \(\emptyset\), ne contient aucun élément, cette condition est automatiquement remplie pour tout ensemble \(B\).

• Élément neutre pour l’union
  L’union d’un ensemble A avec l’ensemble vide Ø est A lui-même, car l’ensemble vide n’ajoute aucun élément. $$ A \cup \emptyset = A $$

  Exemple. Si A = {a, b, c} et B = { } (l’ensemble vide), leur union est simplement A. $$ A \cup B = \{ a,b,c \} \cup \{ \ \} = \{a,b,c \} = A $$ $$ B \cup A = \{ \ \} \cup \{ a,b,c \} = \{a,b,c \} = A $$

• Élément absorbant pour l’intersection
  L’intersection de tout ensemble A avec l’ensemble vide Ø est toujours l’ensemble vide. $$ A \cap \emptyset = \emptyset $$

  Exemple. Si A = {a, b, c} et B = { }, leur intersection est l’ensemble vide. $$ A \cap B = \{ a,b,c \} \cap \{ \ \} = \emptyset $$ $$ B \cap A = \{ \ \} \cap \{ a,b,c \} = \emptyset $$

• Complémentaire
  Le complément de l’ensemble vide dans un ensemble universel \( U \) est \( U \) lui-même.

  $$ U \setminus ∅ = U $$

• Produit cartésien
  Le produit cartésien de tout ensemble A avec l’ensemble vide ∅ est toujours l’ensemble vide. $$ A \times ∅ = ∅ $$ $$ ∅ \times A = ∅ $$
• Ensemble des parties
  L’ensemble des parties de l’ensemble vide ne contient que l’ensemble vide lui-même. $$ P(∅) = \{\emptyset \} $$
• L’ensemble vide est à la fois ouvert et fermé en topologie
  Dans tout espace topologique, l’ensemble vide est considéré comme simultanément ouvert et fermé.
• L’ensemble vide est-il un sous-ensemble propre ou impropre ?
  Selon certains ouvrages de mathématiques, l’ensemble vide (∅) est décrit comme un sous-ensemble impropre, tandis que d’autres le classent parmi les sous-ensembles propres. Cette divergence découle de la définition précise du terme « sous-ensemble propre » adoptée dans chaque contexte.

Et ainsi de suite.