Relations Mathématiques

Qu’est-ce qu’une relation ?

Une relation est une règle qui associe certains éléments de l’ensemble A à un ou plusieurs éléments de l’ensemble B. $$ aRb $$ avec \( a \in A \) et \( b \in B \). On appelle alors \( b \) l’image de \( a \).

Il convient de préciser que l’on parle de « certains » éléments car la règle ne s’applique pas nécessairement à tous les éléments de A.

De même, il n’est pas requis qu’elle concerne l’ensemble complet de B.

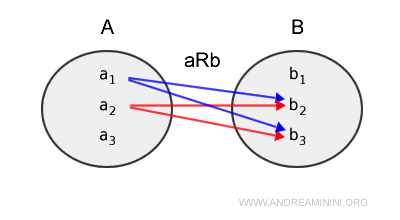
Un même élément de A peut être relié à plusieurs éléments de B.

Le diagramme de Venn précédent peut également être représenté de la manière suivante :

Autrement dit, une relation est simplement un sous-ensemble du produit cartésien AxB.

$$ R \subseteq AxB $$

Remarque : Lorsque A est égal à B, c’est-à-dire \( A = B \), on dit que la relation est définie sur A.

Un exemple concret

Considérons deux ensembles A et B :

$$ A = \{ 2, 4, 6, 8 \} \\ B = \{ 1, 3, 5 \} $$

Le produit cartésien AxB regroupe tous les couples ordonnés (a, b) avec \( a \in A \) et \( b \in B \).

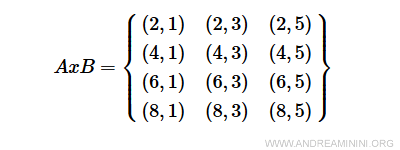
Définissons maintenant une relation R qui associe les couples (a, b) vérifiant la condition \( a + 2b < 10 \).

Par exemple, le couple (2,1) appartient à R puisque \( 2 + 2 \cdot 1 = 4 < 10 \).

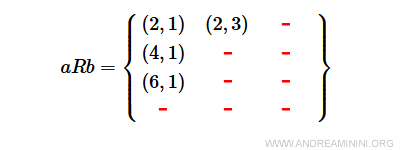
Remarque : Tous les couples (a, b) appartiennent au produit cartésien AxB. Une relation n’est donc qu’un sous-ensemble de ce produit.

La relation R extrait uniquement certains couples parmi tous ceux possibles dans AxB.

Ici, les couples (2,1), (2,3), (4,1) et (6,1) vérifient la condition imposée, les autres non.

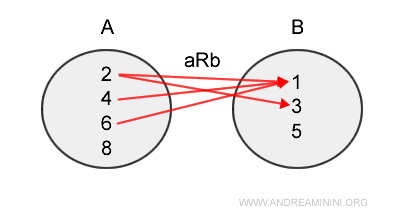
Le sous-ensemble aRb est alors composé des quatre couples suivants :

$$ aRb = \{ (2,1), (2,3), (4,1), (6,1) \} \subset AxB $$

Remarque : Il existe une infinité de relations possibles entre A et B. Celle-ci n’en est qu’un exemple. Si l’on définit une autre relation \( R' \) par \( 2a + b < 10 \), on obtient un sous-ensemble tout à fait différent : $$ aR'b = \begin{Bmatrix} (2,1) & (2,3) & (2,5) \\ (4,1) & - & - \\ - & - & - \\ - & - & - \end{Bmatrix} $$

Exemple

Reprenons les ensembles A et B avec la relation R : a + 2b < 10.

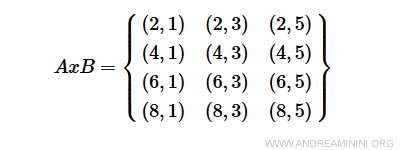
Les éléments de A qui satisfont cette relation sont 2, 4 et 6.

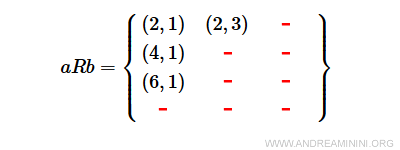
Le domaine de R est donc \( \{2, 4, 6\} \), et le codomaine est \( \{1, 3\} \).

$$ \text{dom(R)} = \{2, 4, 6 \} $$

$$ \text{codom(R)} = \{1, 3 \} $$

Remarque : Dans certains contextes, on considère le domaine comme étant l’ensemble A tout entier, sans distinguer les éléments ayant une image de ceux qui n’en ont pas. Dans ce cas : $$ \text{dom(R)} = \{2, 4, 6, 8 \} $$ Le sous-ensemble de A où R est effectivement définie s’appelle le champ de définition ou domaine effectif de R : $$ \text{champ de définition} = \{2, 4, 6 \} $$

Représentations d’une relation

On peut représenter une relation binaire entre deux ensembles de plusieurs façons :

• Par énumération
  On liste explicitement les couples (a, b) vérifiant la relation. $$ aRb = \{ (2,1), (2,3), (4,1), (6,1) \} $$
• Diagramme fléché
  Représentation graphique classique : chaque flèche relie un élément de A à un ou plusieurs éléments de B.
  

  

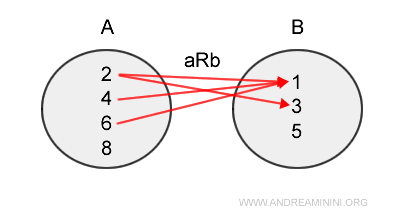
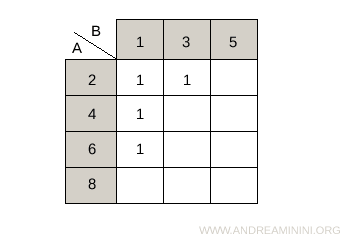
• Matrice de relation (ou tableau à double entrée)
  Une autre méthode consiste à construire une matrice où les lignes correspondent à A et les colonnes à B. On y inscrit :
  • 1 si le couple (a, b) appartient à R,
  • 0 sinon.

  Exemple. Le produit cartésien AxB est :
  
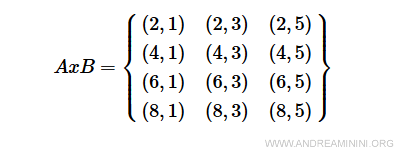
  La relation aRb définie par \( a + 2b < 10 \) est représentée ainsi : $$ aRb = \begin{Bmatrix} 1 & 1 & 0 \\ 1 & 0 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 0 \end{Bmatrix} $$ On peut également utiliser un tableau à double entrée pour une lecture plus intuitive.
  

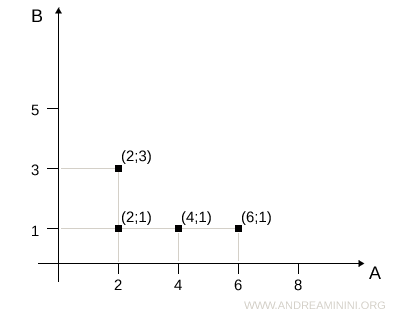
• Représentation cartésienne
  Dans un plan cartésien, les éléments de A sont placés sur l’axe des abscisses et ceux de B sur l’axe des ordonnées. Chaque point représente un couple (a, b) appartenant à la relation.
  

   

La relation inverse

Si l’on a une relation \( b = R(a) \), la relation inverse \( a = R^{-1}(b) \) associe les éléments de B à ceux de A.

La relation \( bR^{-1}a \) existe si et seulement si \( aRb \) existe.

$$ bR^{-1}a \Leftrightarrow aRb $$

Par conséquent :

$$ \text{dom}(R^{-1}) = \text{codom}(R) $$

$$ \text{codom}(R^{-1}) = \text{dom}(R) $$

Exemple

Reprenons la relation R : a + 2b < 10 entre A et B.

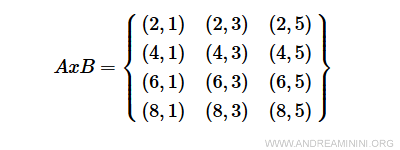
Les éléments de A concernés sont 2, 4 et 6.

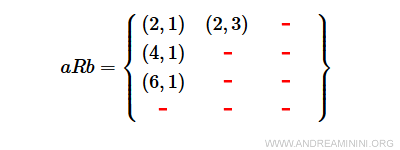
Relation de A vers B :

$$ aRb = \{ (2,1), (2,3), (4,1), (6,1) \} \subset AxB $$

Relation réciproque de B vers A :

$$ bR^{-1}a = \{ (1,2), (3,2), (1,4), (1,6) \} \subset BxA $$

La relation réciproque inverse simplement le sens de l’association initiale.

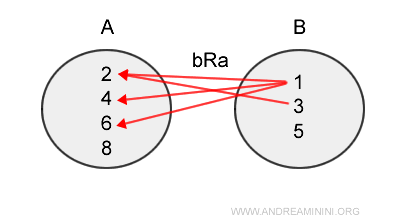
Remarque : Si \( aRb \), alors on a le couple (a, b). Dans \( bR^{-1}a \), ce couple devient (b, a).

Types de relations

On distingue plusieurs catégories de relations :

• Fonctions (ou applications)
• Relations binaires
  Une relation binaire entre deux ensembles A et B est un sous-ensemble du produit cartésien AxB. Elle s’écrit : $$ aRb \quad \text{où} \ a \in A, \ b \in B $$ Chaque élément de la relation est un couple ordonné : $$ (a,b) \in aRb $$
• Relations d’ordre
  Elles vérifient les propriétés de réflexivité, d’antisymétrie et de transitivité.
• Relations d’équivalence
  Elles sont réflexives, symétriques et transitives.
• Relations de compatibilité
  Elles sont réflexives et symétriques, mais pas transitives.

Chaque type de relation possède des propriétés spécifiques.

• Une relation est réflexive si $$ \forall a \in A \Rightarrow (a,a) \in R $$
• Symétrique si $$ \forall (a,b) \in R \Rightarrow (b,a) \in R $$
• Antisymétrique si $$ \forall (a,b) \in R, \ (b,a) \in R \Rightarrow a = b $$
• Transitive si $$ \forall (a,b) \in R, \ (b,c) \in R \Rightarrow (a,c) \in R $$

Ces propriétés sont indépendantes les unes des autres : une relation peut en satisfaire certaines sans nécessairement vérifier les autres.