Relations Antisymétriques

Qu’est-ce qu’une relation antisymétrique ?

Une relation définie sur un ensemble X est dite antisymétrique lorsqu’il est impossible que deux éléments distincts soient liés l’un à l’autre de manière réciproque : $$ aRb,\ a \ne b \ \Rightarrow\ b \require{cancel} \cancel{R}a $$

Autrement dit, dans une relation antisymétrique, si un élément a est en relation avec un élément b (et que \( a \ne b \)), alors l’inverse \( bRa \) ne peut pas être vrai.

Par exemple, la relation « A est supérieur ou égal à B » est antisymétrique : si A ≥ B et A ≠ B, alors il est exclu que B ≥ A.

Cette propriété autorise la réciprocité uniquement dans le cas où les deux éléments sont identiques.

Différence entre antisymétrie et asymétrie - Bien qu’elles soient parfois confondues, ces deux notions expriment des contraintes différentes. Une relation antisymétrique admet la réciprocité à la seule condition que les éléments soient égaux. Une relation asymétrique, en revanche, interdit toute forme de réciprocité, y compris entre un élément et lui-même. Par exemple, la relation « supérieur ou égal à » est antisymétrique : si A ≥ B et A ≠ B, alors B ≥ A ne peut être vrai. Mais cette relation n’est pas asymétrique, puisque lorsque A = B, on a à la fois A ≥ B et B ≥ A - ce qui constitue un couple symétrique.

Les relations antisymétriques constituent une sous-catégorie des relations définies sur un ensemble.

Un Exemple Concret

Considérons l’ensemble suivant :

$$ I = \{ 1, 2, 3, 4 \} $$

Définissons la relation R comme « x est supérieur ou égal à y » :

$$ R = \{ (4;3), (4;2), (4;1), (3;2), (3;1), (2;1) \} $$

Cette relation est antisymétrique, car pour tout couple d’éléments distincts x et y, si \( x \geq y \), alors il n’est jamais vrai que \( y \geq x \).

Remarque. Par exemple, on a bien : $$ 4 \geq 3 $$ mais l’inverse $$ 3 \geq 4 $$ est faux. La relation satisfait donc la condition d’antisymétrie.

Dans une représentation graphique, aucun couple d’éléments distincts n’est relié par deux arcs orientés en sens opposé.

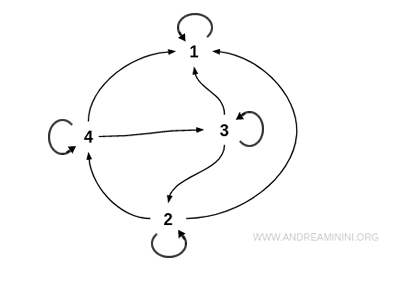
Les seules connexions réciproques observables correspondent à des boucles, représentant des éléments liés à eux-mêmes - comme par exemple \( 3 \geq 3 \).

Contrairement aux relations asymétriques, les boucles sont tout à fait compatibles avec l’antisymétrie, car celle-ci ne concerne que les couples d’éléments distincts.

Remarques Supplémentaires

Quelques précisions importantes sur les relations antisymétriques :

• Une relation peut n’être ni symétrique ni antisymétrique. Ces deux propriétés ne sont ni opposées ni exhaustives.

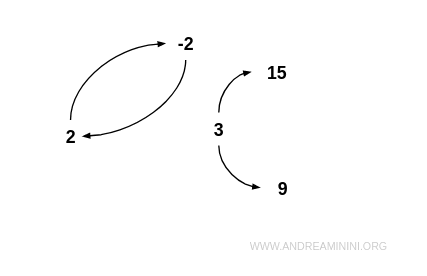
  Exemple. Prenons l’ensemble : $$ I = \{ -2, 2, 3, 9, 15 \} $$ et la relation R définie par « x est un diviseur propre de y » : $$ R = \{ (-2;2), (2;-2), (3;9), (3;15) \} $$ Cette relation n’est pas antisymétrique, car -2 et 2 sont reliés dans les deux sens. Elle n’est pas non plus symétrique, puisque par exemple 9 n’est pas un diviseur de 3. Ainsi, R ne vérifie ni la symétrie ni l’antisymétrie. Dans le graphe correspondant, on observe une paire d’arcs opposés entre -2 et 2, mais pas entre tous les couples.
  

Et ainsi de suite.