Relations Asymétriques

Qu’est-ce qu’une relation asymétrique ?

Une relation définie sur un ensemble X est dite asymétrique lorsqu’à chaque fois qu’un élément a est en relation avec un élément b, l’élément b n’est pas en relation avec a. $$ aRb \ \Rightarrow\ b \require{cancel} \cancel{R}a $$

Dans une relation asymétrique, aucun couple d’éléments distincts ne peut être lié réciproquement.

Par exemple, la relation « A est la mère de B » est asymétrique : si A est la mère de B, alors B ne peut en aucun cas être la mère de A.

Les relations asymétriques appartiennent à la famille des relations définies sur un ensemble.

Un Exemple Concret

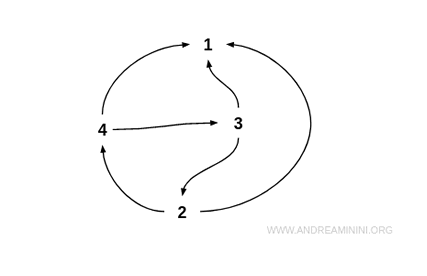
Considérons l’ensemble suivant :

$$ I = \{ 1, 2, 3, 4 \} $$

Définissons R comme la relation « x est strictement supérieur à y » :

$$ R = \{ (4;3), (4;2), (4;1), (3;2), (3;1), (2;1) \} $$

Cette relation est asymétrique car, si x est plus grand que y, alors y ne peut pas être plus grand que x.

Remarque. Par exemple, 4 est supérieur à 3 : $$ 4 > 3 $$ mais 3 n’est pas supérieur à 4 : $$ 3 < 4 $$ La relation vérifie donc bien la propriété d’asymétrie.

Dans une représentation par graphe orienté, une relation asymétrique ne présente jamais deux arcs de sens opposé entre deux sommets distincts.

Asymétrie et Antisymétrie : ne pas confondre

Les notions d’asymétrie et d’antisymétrie sont souvent confondues, bien qu’elles correspondent à des concepts logiquement distincts.

• Relation antisymétrique
• Dans une relation antisymétrique, deux éléments peuvent être en relation dans les deux sens uniquement s’ils sont égaux. Formellement : si \( aRb \) et \( bRa \), alors nécessairement \( a = b \). Autrement dit, si \( a \ne b \), alors \( b \not\!Ra \). $$ aRb ,\ a \ne b \Rightarrow b \require{cancel} \cancel{R} a $$
• Relation asymétrique
• Une relation asymétrique, en revanche, interdit toute réciprocité, même lorsque les deux éléments sont identiques. En particulier, aucun couple \( (a,a) \) n’appartient à la relation. $$ aRb \ \Rightarrow b \require{cancel} \cancel{R} a $$

En résumé : l’antisymétrie tolère la réciprocité uniquement entre éléments identiques, tandis que l’asymétrie l’exclut de manière absolue.

Remarques Complémentaires

Quelques points essentiels à propos des relations asymétriques :

• Toute relation n’est pas nécessairement symétrique ou asymétrique. Le fait qu’une relation ne soit pas asymétrique n’implique pas qu’elle soit symétrique - certaines relations n’ont ni l’une ni l’autre propriété.

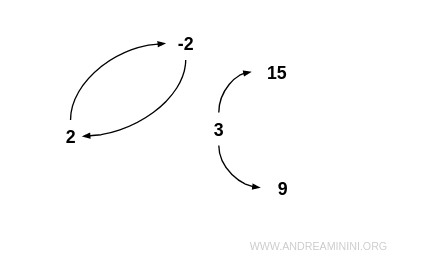
  Exemple. Soit l’ensemble $$ I = \{ -2, 2, 3, 9, 15 \} $$ et la relation R définie par « x est un diviseur propre de y » : $$ R = \{ (-2;2), (2;-2), (3;9), (3;15) \} $$ Cette relation n’est pas asymétrique, puisque -2 et 2 sont reliés mutuellement. Elle n’est pas non plus symétrique, car certaines paires ne sont reliées que dans un seul sens : par exemple, 3 divise 9, mais 9 ne divise pas 3. Ainsi, R n’est ni symétrique ni asymétrique. Dans le graphe correspondant, on observe une paire d’arcs opposés entre -2 et 2, mais pas pour les autres couples.
  

Et ainsi de suite.