Relations Irréflexives

Qu’est-ce qu’une relation irréflexive ?

Une relation définie sur un ensemble I est dite irréflexive (ou encore antiréflexive) lorsqu’aucun élément de l’ensemble n’est en relation avec lui-même. $$ \forall \ a \in I, \ a \require{cancel} \cancel{R} a $$

Autrement dit, dans une relation irréflexive, aucun élément - sans exception - n’est lié à lui-même.

Par exemple, la relation « A est la mère de B » est irréflexive, car personne ne peut être sa propre mère.

Les relations irréflexives forment une sous-catégorie spécifique des relations définies sur un ensemble.

Un Exemple Concret

Considérons l’ensemble fini I :

$$ I = \{ 2,4,3,9,16 \} $$

Définissons une relation R qui associe à chaque élément sa racine carrée, autrement dit : « x est la racine carrée de y ».

$$ R = \{ (4;2), (16;4), (9;3) \} $$

Cette relation est irréflexive, car aucun des éléments de I n’est la racine carrée de lui-même.

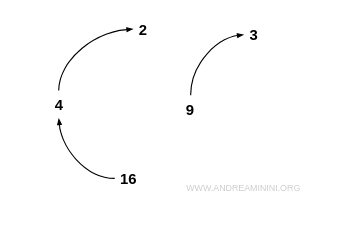
Remarque. Par exemple, 2 n’est pas la racine carrée de 2. $$ 2 \ne \sqrt{2} $$ Il en va de même pour tous les autres éléments de I. Dans une représentation par graphe, une relation irréflexive se caractérise par l’absence totale de boucles : aucun nœud ne possède d’arête qui le relie à lui-même.

Remarques Supplémentaires

Voici quelques observations importantes à propos des relations irréflexives:

• Il existe des relations qui ne sont ni réflexives ni irréflexives. Autrement dit, le fait qu’une relation ne soit pas irréflexive n’implique pas nécessairement qu’elle soit réflexive, et réciproquement.

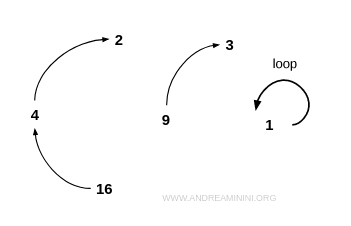
  Exemple. Considérons l’ensemble $$ I = \{1,2,3,4,9,16 \} $$ et la relation R définie par « x est la racine carrée de y ». Cette relation n’est pas réflexive, puisque tous les éléments ne sont pas reliés à eux-mêmes - par exemple, 2 n’est pas la racine carrée de 2. $$ 2 \ne \sqrt{2} $$ Mais elle n’est pas non plus irréflexive, car elle contient au moins un couple réflexif : par exemple, 1 est la racine carrée de 1. $$ 1 = \sqrt{1} $$ Dans le graphe associé, le nœud correspondant à 1 possède une boucle. Cela montre que la relation n’est pas irréflexive. Toutefois, comme tous les nœuds n’ont pas de boucle, elle n’est pas réflexive non plus.
  

Et ainsi de suite.