Relations Symétriques

Qu’est-ce qu’une relation symétrique ?

Une relation est dite symétrique lorsque, chaque fois qu’un élément a est en relation avec un élément b, l’élément b est également en relation avec a. $$ \forall a,b \in X \ , \ aRb \Rightarrow bRa $$

On parle de relations symétriques car leur représentation graphique met en évidence une structure en miroir, parfaitement équilibrée de part et d’autre de la diagonale.

Par exemple, si X est le frère de Y, alors Y est aussi le frère de X.

Les relations symétriques constituent une sous-catégorie particulière des relations définies sur un ensemble.

Remarque. Une relation symétrique devient une relation d’équivalence si elle est également réflexive et transitive.

Un Exemple Concret

Considérons l’ensemble suivant :

$$ A = \{ -1, -2, -3, 1, 2, 3 \} $$

On définit une relation R qui associe à chaque nombre son opposé additif.

$$ R = \{ (-1;1), (-2;2), (-3;3), (1;-1), (2;-2), (3;-3) \} $$

Cette relation est un sous-ensemble du produit cartésien AxA.

Elle peut être représentée au moyen d’un tableau à double entrée.

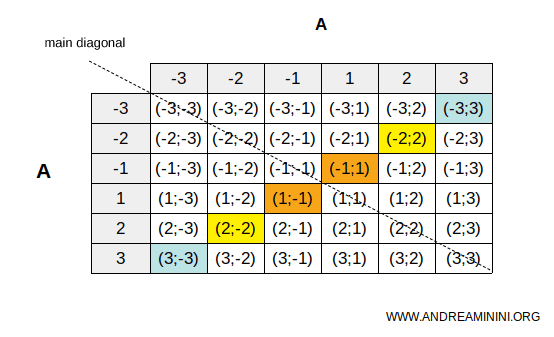
Ce tableau révèle une symétrie manifeste par rapport à la diagonale principale.

Chaque case qui satisfait la relation (signalée en couleur) possède son symétrique par rapport à la diagonale, également présent dans la relation et mis en évidence de manière identique.

Par exemple, -2 est l’opposé de 2, et inversement, 2 est l’opposé de -2.

Cette symétrie devient encore plus évidente lorsqu’on trace la relation dans le plan cartésien.

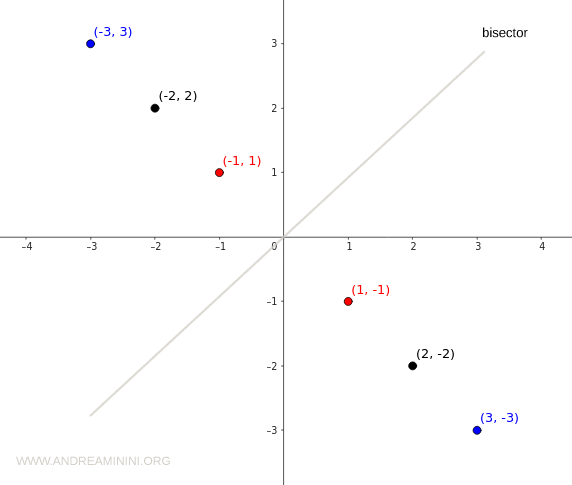
Dans ce type de représentation, la symétrie se reflète le long de la bissectrice.

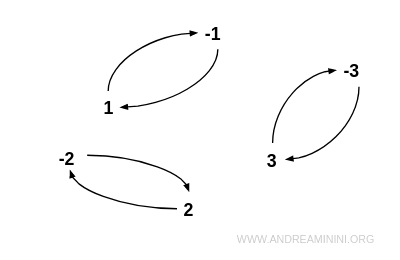
Remarque. Dans un graphe orienté, une relation est symétrique si toute arête dirigée entre deux sommets est accompagnée de son arête inverse, de sens opposé.

Autres Exemples

• La relation « x est perpendiculaire à y » est symétrique, car si une droite x est perpendiculaire à une droite y, alors y est aussi perpendiculaire à x.

Éléments Complémentaires

Quelques points essentiels à retenir sur les relations symétriques :

• Le fait qu’une relation ne soit pas symétrique ne signifie pas pour autant qu’elle est asymétrique : certaines relations ne vérifient ni l’une ni l’autre de ces propriétés.
• La symétrie n’est pas l’inverse de l’antisymétrie : une relation peut très bien ne posséder ni l’une ni l’autre.

Et ainsi de suite.