Relations d’ordre

Les relations d’ordre sont des relations mathématiques qui vérifient trois propriétés essentielles : la réflexivité, l’antisymétrie et la transitivité.

• Réflexivité : $$ \forall \ a \in A \:\: a\rho a $$
• Antisymétrie : $$ \forall \ a,b \in A \ , \ a\rho b , \ a \ne b \Rightarrow b \require{cancel} \cancel{\rho} a $$
• Transitivité : $$ \forall \ a,b,c \in A :\: [ a\rho b \land b\rho c ] \rightarrow a\rho c $$

Ces relations sont également appelées ordres larges (ou non stricts).

On distingue aussi les ordres stricts, dans lesquels la réflexivité est remplacée par l’irréflexivité.

De manière générale, une relation est considérée comme une relation d’ordre lorsqu’elle est réflexive (ou irréflexive), antisymétrique et transitive.

Exemple concret

Examinons l’ensemble des entiers naturels :

$$ N = \{ 1, 2, 3, 4, ... \} $$

Nous voulons déterminer si la relation R : « x est un multiple de y » constitue une relation d’ordre.

Pour cela, analysons si elle satisfait les trois propriétés fondamentales :

• Réflexivité : Tout entier est multiple de lui-même (par exemple, x = 1·x).
• Antisymétrie : Si x et y sont distincts et que x est un multiple de y, alors y ne peut pas être un multiple de x.
• Transitivité : Si x est un multiple de y et y un multiple de z, alors x est un multiple de z.

Puisque les trois conditions sont remplies, R est bien une relation d’ordre.

Ordres stricts et ordres larges

Les relations d’ordre se répartissent en deux grandes catégories :

• Relations d’ordre large
  Elles vérifient la réflexivité, l’antisymétrie et la transitivité.

  Exemple : La relation « x est un multiple de y » est un ordre large. Elle est réflexive (tout entier est multiple de lui-même, comme 2·1=2 ou 3·1=3), et elle satisfait également l’antisymétrie et la transitivité.

• Relations d’ordre strict
  Elles satisfont l’irréflexivité, l’antisymétrie et la transitivité.

  Exemple : La relation « x est plus grand que y » est un ordre strict. Elle est irréflexive (aucun élément n’est strictement supérieur à lui-même), et elle est aussi antisymétrique et transitive.

En résumé, les ordres stricts sont irréflexifs, tandis que les ordres larges sont réflexifs.

Ordres partiels et totaux

Qu’ils soient stricts ou larges, les ordres peuvent être classés selon le degré de comparabilité qu’ils induisent sur un ensemble. Une relation d’ordre peut ainsi être partielle ou totale :

• Ordre partiel

  Un ordre partiel permet de comparer uniquement certains couples d’éléments, ce qui signifie que tous les éléments ne sont pas nécessairement comparables entre eux.

  Il est défini sur un sous-ensemble du produit cartésien. On parle alors d’un ensemble partiellement ordonné, car seuls certains couples d’éléments y sont comparables.

  Exemple : L’ensemble des parties P(X), avec X = {1, 2, 3}, contient les sous-ensembles suivants : {∅, {1}, {2}, {3}, {1,2}, {1,3}, {2,3}, {1,2,3}}. Sous la relation d’inclusion ⊆, on obtient un ordre partiel : par exemple, {1} ⊆ {1,2}, tandis que {3} n’est pas inclus dans {1,2}. Cette structure peut être représentée ainsi :
  

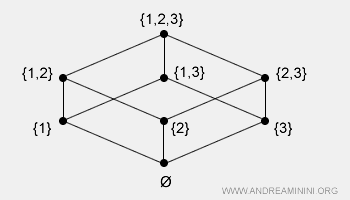
• Ordre total

  Un ordre total permet de comparer tous les couples d’éléments de l’ensemble : chaque paire d’éléments est comparable.

  Il s’applique à tous les couples (a, b) de l’ensemble. Dans ce cas, l’ensemble est qualifié de totalement ordonné ou de chaîne, en raison de sa structure linéaire : tout élément est comparable à tout autre.

  Exemple : L’ensemble X = {1, 2, 3} peut être totalement ordonné via la relation ≤ (ou ≥). Tous les couples sont comparables : 1ρ2, 2ρ3, 1ρ3, etc. Le diagramme associé forme une chaîne, chaque élément y étant lié aux autres.
  

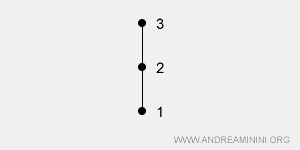
Représentation graphique des relations d’ordre

Les relations d’ordre sur un ensemble X peuvent être représentées graphiquement par des diagrammes de points reliés entre eux par des segments.

Chaque point représente un élément de l’ensemble.

Un segment relie deux éléments lorsqu’ils sont immédiatement comparables, c’est-à-dire qu’il n’existe aucun élément intermédiaire entre eux.

Exemple : Dans la relation ≤, les éléments 1 et 3 sont bien comparables. Toutefois, comme 2 se trouve entre les deux, il n’y a pas de segment direct entre 1 et 3. En revanche, 1 est relié à 2, et 2 à 3, car aucun élément ne s’intercale entre eux.

Ensembles ordonnés isomorphes

Deux ensembles ordonnés sont dits isomorphes lorsqu’ils possèdent une structure d’ordre identique, c’est-à-dire que les relations entre leurs éléments respectifs se correspondent.

Par exemple, tout couple d’ensembles totalement ordonnés de même cardinalité sera toujours isomorphe.

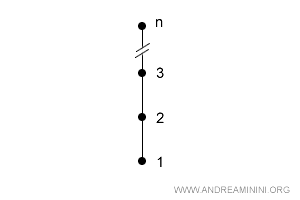
En définitive, deux ensembles isomorphes partagent une même structure d’ordre, même si leurs éléments diffèrent.

Et ainsi de suite.