Relations Réflexives
Qu’est-ce qu’une relation réflexive ?
Une relation définie sur un ensemble A est dite réflexive lorsque chaque élément de A est relié à lui-même. $$ \forall \ a \in A, \ aRa $$
Autrement dit, une relation réflexive établit un lien systématique entre chaque élément de l’ensemble et lui-même.
Par exemple, la relation « X a le même âge que Y » est réflexive, puisqu’une personne a forcément le même âge qu’elle-même.
Les relations réflexives font partie de la famille plus large des relations définies sur un ensemble.
Un Exemple Concret
Considérons l’ensemble suivant :
$$ A = \{ 2,3,4,5,6,7,8,9 \} $$
On définit une relation R qui associe à chaque élément de A ses multiples, à condition qu’ils appartiennent également à A.
$$ R = \{ (2;2), (2;4), (2;6), (2;8), (3;3), (3;6), (3;9)\\ \ \ \ \ \ \ \ \ \ \ \ \ (4;4), (4;8), (5;5), (6;6), (7;7), (8;8), (9;9) \} $$
Cette relation constitue un sous-ensemble du produit cartésien A × A, c’est-à-dire l’ensemble de tous les couples ordonnés formés d’éléments de A.
On peut représenter cette relation à l’aide d’un tableau à double entrée.
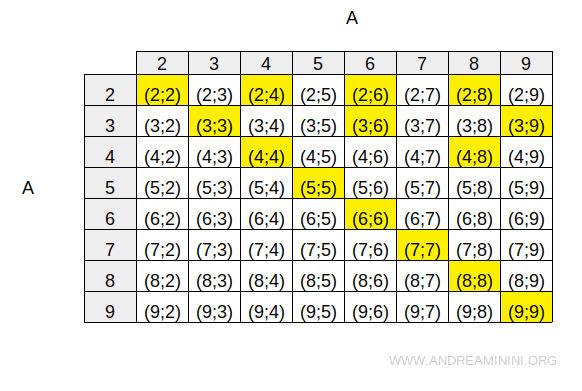
Les cases colorées en jaune indiquent les couples de A × A qui vérifient la relation R.
On constate que chaque élément est bien relié à lui-même.
La diagonale principale du tableau ne contient que des couples de la forme (a ; a) appartenant à R (mis en évidence en jaune), comme (2 ; 2), (3 ; 3), (4 ; 4), etc.
Ce constat confirme que R est bien une relation réflexive.
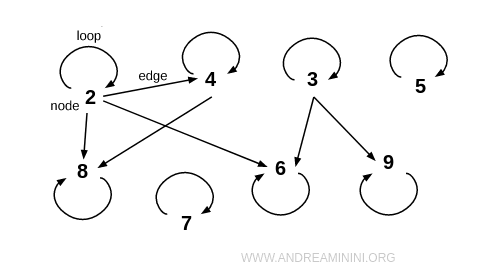
Remarque. Dans une représentation en graphe, une relation est réflexive si chaque nœud possède une boucle, c’est-à-dire une arête orientée qui part du nœud et revient sur lui-même. Cette propriété visuelle permet d’identifier immédiatement la réflexivité.
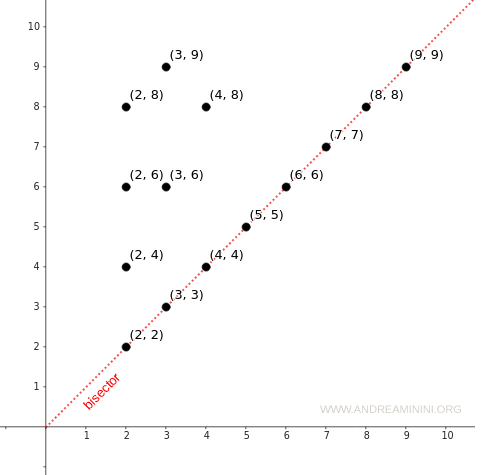
Dans un diagramme cartésien, une relation est réflexive lorsque tous les éléments de A apparaissent sous forme de couples (a ; a) alignés sur la diagonale (la bissectrice). Là encore, la réflexivité saute aux yeux.
Autres Exemples
- La relation « x est perpendiculaire à y » n’est pas réflexive, puisqu’aucune droite ne peut être perpendiculaire à elle-même.
Et ainsi de suite.