Relations transitives
Qu’est-ce qu’une relation transitive ?
Une relation est dite transitive lorsque, pour tous éléments a, b et c d’un ensemble I, si a est en relation avec b et b en relation avec c, alors a est nécessairement en relation avec c. $$ \forall \ a,b,c \in I \ | \ aRb \ , \ bRc \ \Rightarrow aRc $$ Cette propriété peut être illustrée graphiquement de la manière suivante :
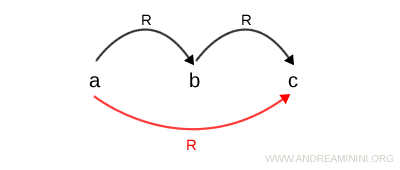
On parle de relation transitive car elle respecte la propriété de transitivité.
Par exemple, si A est le frère de B et que B est le frère de C, alors A est aussi le frère de C.
Les relations transitives font partie de la catégorie plus large des relations définies sur un ensemble.
Remarque : Une relation n’est pas nécessairement transitive. Par exemple, si A est la mère de B et B est la mère de C, cela ne signifie pas que A est la mère de C. Cette relation n’est donc pas transitive.
Un exemple concret
Considérons l’ensemble I :
$$ I = \{ 2 , 4, 6, 8, 10 \} $$
La relation R relie des paires de nombres pairs.
Par exemple, 2 et 4 sont liés car ce sont tous deux des nombres pairs :
$$ 2R4 $$
De même, 4 et 6 sont également en relation pour la même raison :
$$ 4R6 $$
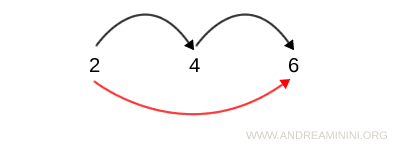
En vertu de la transitivité, 2 et 6 doivent aussi être en relation : si 2 est lié à 4 et que 4 est lié à 6, alors 2 est nécessairement lié à 6 :
$$ 2R6 $$
Dans cet exemple, la propriété de transitivité est vérifiée pour toutes les combinaisons possibles d’éléments de l’ensemble I = {2, 4, 6, 8, 10}.
On peut donc conclure que la relation R est transitive sur l’ensemble I.
Remarque : Les relations transitives sont souvent représentées à l’aide de graphes. Dans ce type de représentation, il est facile d’identifier la transitivité en observant les liens entre les nœuds (les éléments de l’ensemble). Par exemple, s’il existe une flèche de 2 vers 4 et une autre de 4 vers 6, on doit également trouver une flèche directe de 2 vers 6.
En revanche, les tableaux à double entrée ou les diagrammes cartésiens rendent cette propriété moins évidente à détecter.
Autres exemples
- La relation « x est perpendiculaire à y » n’est PAS transitive. Si la droite x forme un angle de 90° avec la droite y, et que y forme à son tour un angle de 90° avec la droite z, alors x et z forment un angle de 180° (elles sont alignées) ou de 0° (elles coïncident). Dans les deux cas, x et z ne sont pas perpendiculaires.