Relation inverse

Étant donnée une relation aRb définie sur le produit cartésien A×B, sa relation inverse bR^-1a est le sous-ensemble de B×A formé de tous les couples (b, a) tels que la relation aRb soit satisfaite.

Autrement dit, si aRb est une relation allant de l’ensemble A vers l’ensemble B, alors la relation inverse bR^-1a établit un lien en sens inverse, de B vers A.

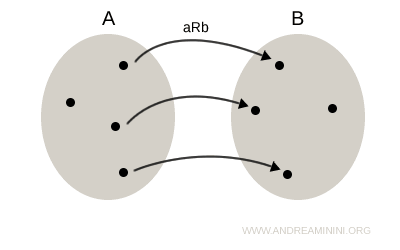
On construit la relation inverse R^-1 en inversant l’ordre des éléments dans chaque couple (a, b), ce qui donne les couples (b, a).

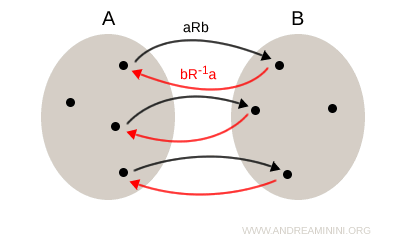
Graphiquement, la relation inverse se représente en inversant le sens des flèches : à chaque flèche aRb allant de A vers B correspond une flèche bR^-1a allant de B vers A.

Il en résulte que le domaine de la relation inverse correspond au codomaine de la relation initiale :

$$ \text{domaine} \ R^{-1} = \text{codomaine} \ R $$

Et son codomaine coïncide avec le domaine de la relation de départ :

$$ \text{codomaine} \ R^{-1} = \text{domaine} \ R $$

Remarque : La relation inverse bR^-1a est vérifiée si et seulement si la relation directe aRb l’est également. $$ bR^{-1}a \Leftrightarrow aRb $$

Un exemple concret

Considérons deux ensembles finis A et B :

$$ A = \{2,3,4,5,6 \} $$

$$ B = \{4,9,16,25,36 \} $$

La relation R associe à chaque élément de A son carré dans B :

$$ aRb \ : \ b = a^2 $$

Il s’agit d’un sous-ensemble du produit cartésien A×B, composé des couples ordonnés (a, b) suivants :

$$ aRb = \{ (2,4), (3,9), (4,16), (5,25), (6,36) \} \subset A×B $$

Voici le diagramme sagittal illustrant la relation aRb :

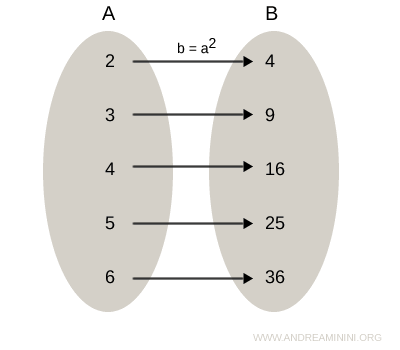
La relation inverse R^-1 associe...