Relations Définies sur un Ensemble

On dit qu’une relation est définie sur un ensemble lorsqu’elle associe entre eux des éléments d’un même ensemble A.

Dans ce cadre, le domaine et le codomaine sont identiques.

Un tel type de relation constitue un sous-ensemble du produit cartésien A × A.

Un Exemple Concret

Considérons l’ensemble fini suivant :

$$ A = \{ 2,3,4,5,6,7,8,9 \} $$

Le produit cartésien de A avec lui-même, noté A × A, se présente ainsi :

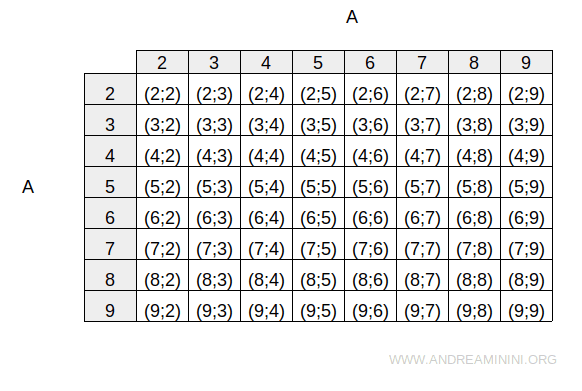
Définissons une relation R sur A qui associe à chaque élément ses multiples :

$$ R = \{ (2;2) , (2;4),(2;6),(2;8),(3;3),(3;6),(3;9)\\ \ \ \ \ \ \ \ \ \ \ \ \ (4;4) , (4;8),(5;5),(6;6),(7;7),(8;8),(9;9) \} $$

Cette relation constitue donc un sous-ensemble du produit cartésien A × A.

Voyons à présent comment cette relation peut être représentée sous forme de tableau à double entrée :

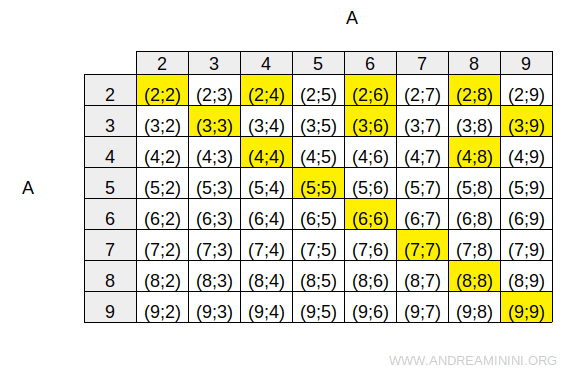
Le diagramme fléché (aussi appelé diagramme de correspondance) associé à cette relation est le suivant :

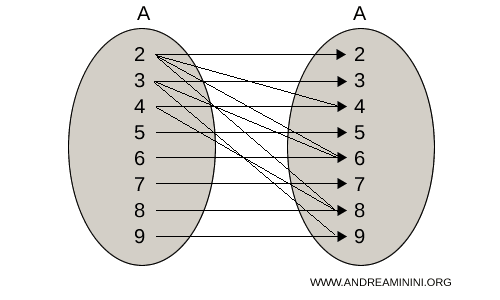
Dans ce cas, l’ensemble A joue simultanément le rôle de domaine et de codomaine.

Examinons maintenant le diagramme cartésien correspondant :

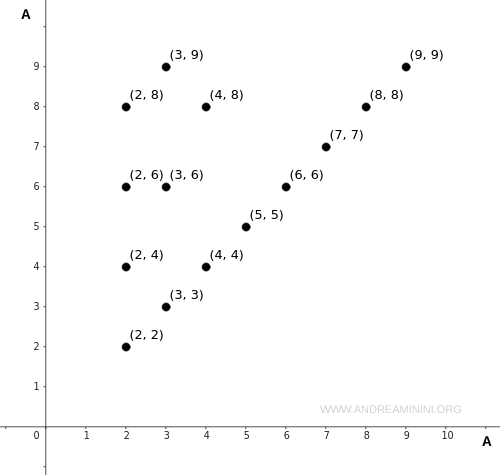
Comme on peut le voir, l’ensemble A est reporté à la fois sur l’axe horizontal (axe x) et sur l’axe vertical (axe y).

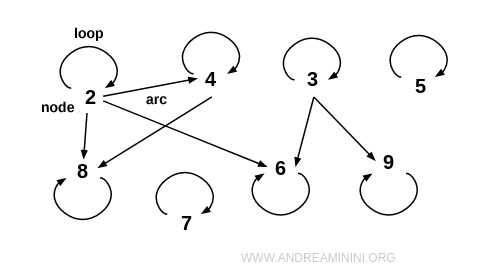
Remarque. Les relations définies sur un ensemble peuvent être représentées de manière plus visuelle à l’aide d’un graphe. Il suffit de représenter chaque élément de A par un nœud, sans encadrement, et de tracer des arcs orientés entre les éléments en relation. Lorsqu’un élément est relié à lui-même - comme dans le cas de (2;2) - on obtient un arc particulier appelé boucle. En règle générale, les représentations graphiques sont plus claires, compactes et efficaces sur le plan visuel.

Types de Relations Définies sur un Ensemble

Parmi les relations que l’on peut définir sur un ensemble, on distingue plusieurs catégories fondamentales :

• Relation Réflexive
  Une relation R sur un ensemble A est dite réflexive si tout élément a ∈ A est relié à lui-même. $$ \forall \ a \in A \Rightarrow \ aRa $$
• Relation Irréflexive
  R est dite irréflexive si aucun élément a ∈ A n’est en relation avec lui-même. $$ \forall \ a \ \in A \ \Rightarrow a \require{cancel} \cancel{R} a $$
• Relation Symétrique
  R est symétrique si, pour tous a et b dans A, le fait que a soit en relation avec b implique que b le soit aussi avec a. $$ aRb \ \Leftrightarrow \ bRa $$
• Relation Asymétrique
  R est asymétrique si, pour tous a et b dans A, si a est en relation avec b, alors b n’est pas en relation avec a. $$ aRb \Rightarrow b \require{cancel} \cancel{R} a $$
• Relation Antisymétrique
  R est antisymétrique si, pour tous les éléments a et b de A tels que a ≠ b, le fait que a soit en relation avec b implique que b ne l’est pas avec a. $$ aRb , \ a \ne b \Rightarrow b \require{cancel} \cancel{R} a $$

  Quelle est la différence entre asymétrie et antisymétrie ? Une relation antisymétrique autorise une réciprocité uniquement lorsque les éléments sont égaux. Autrement dit, si a est en relation avec b et b avec a, alors nécessairement a = b. $$ aRb , \ a \ne b \Rightarrow b \require{cancel} \cancel{R} a $$ En revanche, une relation asymétrique exclut toute réciprocité, même entre un élément et lui-même. $$ aRb \Rightarrow b \require{cancel} \cancel{R} a $$ En résumé, l’asymétrie interdit toute relation réciproque, tandis que l’antisymétrie les autorise seulement dans le cas où les éléments sont identiques.

• Relation Transitive
  Une relation R définie sur un ensemble A est transitive si, chaque fois que a est en relation avec b et b avec c, alors a est aussi en relation avec c. $$ aRb , \ bRc \Rightarrow aRc $$

Et ainsi de suite.