Ensemble compact
Dans un espace tel que \(\mathbb{R}^n\), un ensemble compact est un ensemble à la fois fermé et borné.
- Fermé : un ensemble est fermé s’il contient tous ses points limites, c’est-à-dire s’il inclut l’ensemble de sa frontière.
- Borné : un ensemble est borné s’il est entièrement contenu dans une boule de rayon fini.
Dans un cadre plus général, c’est-à-dire en topologie, un ensemble \(K\) est dit compact si toute couverture ouverte de \(K\) admet une sous-couverture finie qui le recouvre encore entièrement.
Dans \(\mathbb{R}^n\), ces deux définitions sont équivalentes. En revanche, elles peuvent différer dans des espaces topologiques plus abstraits.
Remarque : La compacité confère à l’ensemble des propriétés essentielles, telles que le fait qu’une fonction continue y atteint nécessairement un maximum et un minimum (théorème de Weierstrass), ou encore que toute suite y possède une sous-suite convergente (théorème de Bolzano-Weierstrass). En particulier, toute fonction continue définie sur un ensemble compact admet toujours des extrema, sans exception.
Exemples
Exemple 1
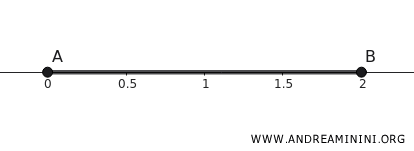
Considérons l’intervalle \([0,2]\) sur la droite réelle \(\mathbb{R}\).
On définit l’ensemble suivant :
\[ K = \{ x \in \mathbb{R} \mid 0 \leq x \leq 2 \} \]
Cet ensemble est compact pour les raisons suivantes :
- Il est fermé, car il contient ses bornes \(0\) et \(2\).
- Il est borné, puisque tous ses éléments sont compris entre \(0\) et \(2\), et donc il ne s’étend pas indéfiniment.
Exemple 2
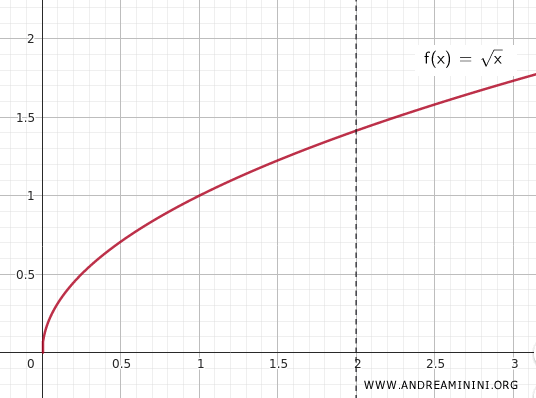
Considérons à présent la fonction continue \(f(x) = \sqrt{x}\) définie sur \(K\).
Comme \(f(x)\) est continue sur un ensemble compact, le théorème de Weierstrass garantit qu’elle atteint un minimum et un maximum sur \(K\).
En effet, sur l’intervalle \([0,2]\), la fonction atteint son minimum en \(x = 0\) (valeur \(0\)) et son maximum en \(x = 2\) (valeur \(\sqrt{2}\)).
Exemple 3
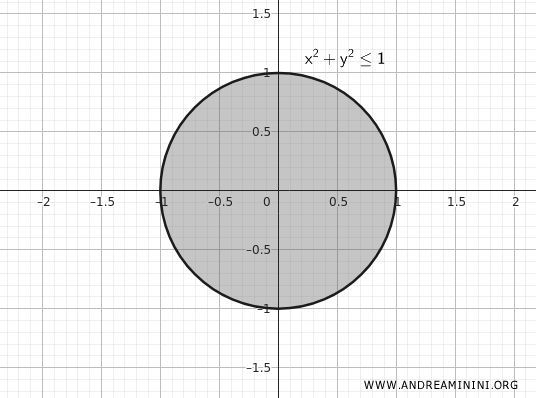
Examinons maintenant le disque fermé de rayon \(1\), centré à l’origine du plan \(\mathbb{R}^2\).
On définit l’ensemble suivant :
\[ K = \{ (x,y) \in \mathbb{R}^2 \mid x^2 + y^2 \leq 1 \} \]
Cet ensemble est également compact pour les raisons suivantes :
- Il est fermé, car il contient tous les points de la frontière définie par \(x^2 + y^2 = 1\).
- Il est borné, puisqu’aucun point ne se trouve à une distance supérieure à \(1\) de l’origine \((0,0)\).
Et ainsi de suite.