Ensemble partiellement ordonné

Un ensemble muni d’un ordre partiel est appelé un ensemble partiellement ordonné, ou plus simplement un poset. On le note sous la forme (A, ≤).

Que signifie « ordre partiel » ?

Soit A un ensemble. Un ordre partiel est une relation

$$ ≤:A \times A \rightarrow \{ \text{vrai}, \text{faux} \}. $$

Autrement dit, pour chaque paire (x, y) d’éléments de A, on peut déterminer si la relation d’ordre ≤ est vérifiée.

Un exemple concret

Considérons un ensemble fini A composé de sept éléments :

$$ A = \{ a, b, c, d, e, f \} $$

On définit une relation ≤ sur le produit cartésien A × A :

$$ ≤ = \{ (a,c), (a,e), (b,d), (b,f), (c,g), (d,g), (e,g), (f,g) \} $$

Le couple (A, ≤) constitue donc un poset.

Remarque : La relation n’est pas définie pour toutes les paires d’éléments. Par exemple, il n’existe aucune relation entre (a, b), (a, d), etc.

Les relations d’ordre dans le poset (A, ≤) peuvent être représentées à l’aide du graphe suivant :

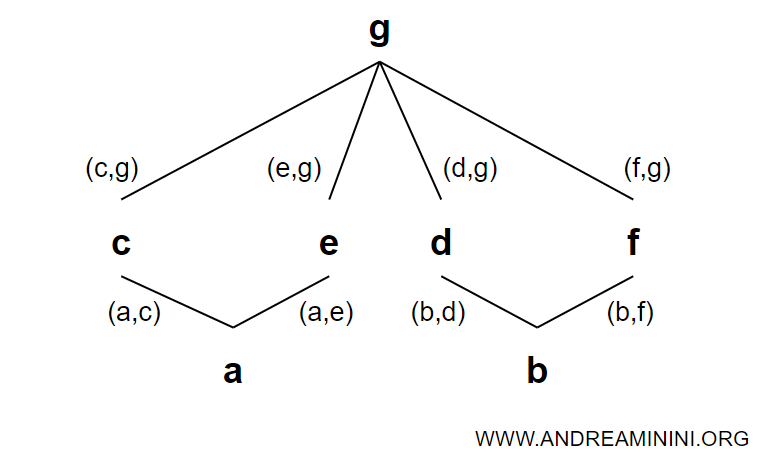
Chaque flèche indique qu’un élément est inférieur ou égal à un autre selon la relation définie.

Autres exemples de posets

• Les entiers naturels
  L’ensemble \( (\mathbb{N}, \leq) \), constitué des entiers naturels munis de l’ordre usuel « inférieur ou égal », forme un poset. Cette relation satisfait les propriétés de réflexivité, d’antisymétrie et de transitivité.

  Par exemple, pour tout couple d’éléments dans \( \mathbb{N} = \{0, 1, 2, 3, \dots\} \), il est toujours possible de comparer les deux éléments selon l’ordre ≤.

• L’ensemble des parties ordonné par inclusion
  Si \( S \) est un ensemble, son ensemble des parties \( \mathcal{P}(S) \) - c’est-à-dire l’ensemble de tous ses sous-ensembles - forme un poset sous la relation d’inclusion (\(\subseteq\)). Ici, l’ordre ne repose pas sur des valeurs numériques mais sur des relations d’inclusion.
  

  Par exemple, si \( S = \{a, b\} \), alors \( \mathcal{P}(S) = \{\emptyset, \{a\}, \{b\}, \{a, b\}\} \). L’ensemble vide Ø est inclus dans tous les autres, et {a} comme {b} sont inclus dans {a, b}. En revanche, {a, b} n’est inclus ni dans {a}, ni dans {b}. $$ \emptyset \subseteq \{ a \} \\ \{ a \} \subseteq \{a, b\} \\ \{ b \} \subseteq \{a, b\} \\ \vdots $$ Ces relations peuvent être représentées à l’aide d’un diagramme en treillis, où chaque nœud correspond à un sous-ensemble, et les arêtes indiquent les inclusions, orientées du bas vers le haut.
  

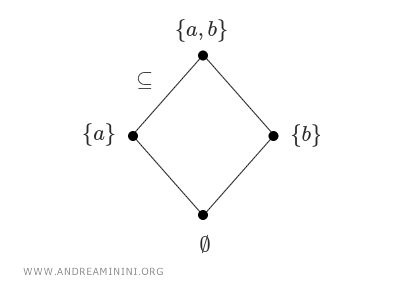
• La divisibilité dans les entiers
  Un autre exemple classique de poset est l’ensemble \( \mathbb{Z} \), muni de la relation de divisibilité. On dit que \( x \mid y \) si x divise y, ce qui définit un ordre partiel dans certains sous-ensembles de \( \mathbb{Z} \).
  

  Par exemple, 4 divise 8 (donc 4 | 8 est vrai), tandis que 6 ne divise pas 8 (6 | 8 est faux). Prenons le sous-ensemble S = {2, 4, 6, 8, 12, 24}. Le diagramme de Hasse correspondant représente chaque nombre par un nœud, avec des arêtes reliant les diviseurs à leurs multiples, du bas vers le haut.
  
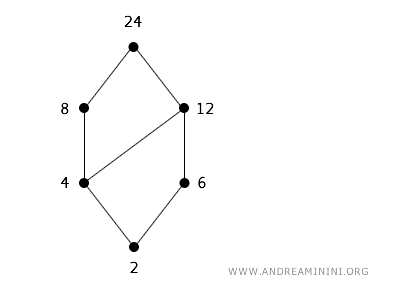
  Dans ce cas, 2 divise tous les autres éléments : 4, 6, 8, 12 et 24. En revanche, 6 ne divise que 12 et 24, mais pas 2, 4 ni 8.

Propriétés fondamentales d’un poset

Un poset est un couple (S, ≤) où S est un ensemble et ≤ une relation binaire vérifiant les trois propriétés suivantes :

• Réflexivité : Tout élément est en relation avec lui-même : $$ \forall x \in S,\ x \le x $$
• Antisymétrie : Si deux éléments sont liés dans les deux sens, alors ils sont égaux : $$ \forall x, y \in S,\ (x \le y \land y \le x) \Rightarrow x = y $$
• Transitivité : Si x ≤ y et y ≤ z, alors x ≤ z : $$ \forall x, y, z \in S,\ (x \le y \land y \le z) \Rightarrow x \le z $$

En résumé, un poset est un ensemble muni d’une relation réflexive, antisymétrique et transitive, mais qui n’est pas nécessairement totale. Autrement dit, il n’est pas requis que tous les éléments soient comparables deux à deux.

Les ensembles partiellement ordonnés jouent un rôle fondamental en théorie des treillis, et apparaissent dans des domaines comme l’algèbre commutative (par exemple, dans l’ensemble des idéaux d’un anneau) ou la topologie algébrique.

Infimum et supremum

Soit (A, ≤) un poset, et B un sous-ensemble de A :

• L’infimum de B, noté inf(B), est le plus grand élément de A qui est inférieur ou égal à tous les éléments de B.
• Le supremum de B, noté sup(B), est le plus petit élément de A qui est supérieur ou égal à tous les éléments de B.

Exemple

Le sous-ensemble B admet pour infimum l’élément 3 et pour supremum l’élément 4.

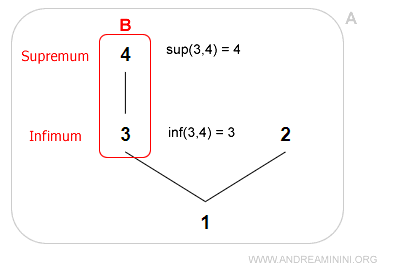
Remarque : Un sous-ensemble ne possède pas toujours un infimum ou un supremum, mais s’ils existent, ils sont nécessairement uniques.

Bornes inférieure et supérieure

Soit (A, ≤) un poset, et B un sous-ensemble de A :

• Un élément \( k \in A \) est une borne inférieure de B si \( k \le b \) pour tout \( b \in B \).

  Exemple : si A = {1, 2, 3, 4, 5, 6} et B = {3, 4}, alors les bornes inférieures de B sont {1, 2, 3}.

• Un élément \( k \in A \) est une borne supérieure de B si \( k \ge b \) pour tout \( b \in B \).

  Exemple : avec les mêmes ensembles A et B, les bornes supérieures de B sont {4, 5, 6}.

Éléments maximaux et minimaux

Dans un poset (A, ≤) :

• Un élément minimal est un élément qui n’est précédé par aucun autre dans A.

  Exemple : dans A = {1, 2, 3, 4, 5, 6}, l’élément minimal est 1.

• Un élément maximal est un élément qui n’est suivi par aucun autre élément de A.

  Exemple : dans ce même ensemble, l’élément maximal est 6.

Un poset peut admettre plusieurs éléments maximaux ou minimaux.

Exemple

Le diagramme suivant illustre un cas avec trois éléments maximaux et un unique élément minimal.

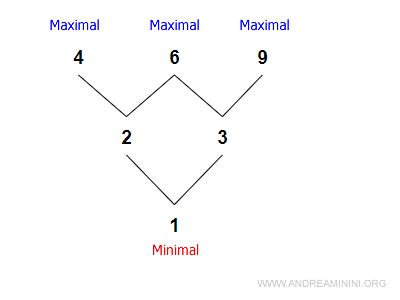
La relation d’ordre considérée est :

$$ ≤ = \{ (1,2), (1,3), (2,4), (2,6), (3,6), (3,9) \} $$

On en déduit :

• 4, 6 et 9 n’ont pas de successeur dans A : ce sont des éléments maximaux.
• 1 n’a aucun prédécesseur : c’est l’élément minimal.

Remarque : Dans un poset infini, des éléments maximaux ou minimaux peuvent ne pas exister. En revanche, tout poset fini admet au moins un élément de chaque type.

Maximum et minimum

Dans un poset (A, ≤) :

• Le minimum est l’unique élément qui est inférieur ou égal à tous les autres éléments de A.
• Le maximum est l’unique élément qui est supérieur ou égal à tous les autres éléments de A.

Un poset ne possède pas nécessairement de minimum ni de maximum.

Exemple

Dans le cas suivant, 1 est le minimum, mais il n’existe pas de maximum.

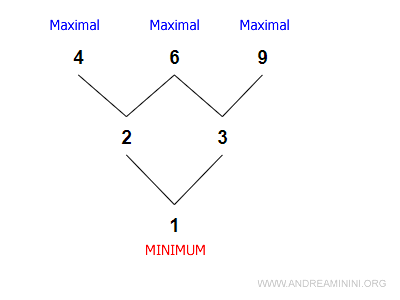
La relation d’ordre est la suivante :

$$ ≤ = \{ (1,2), (1,3), (2,4), (2,6), (3,6), (3,9) \} $$

On vérifie que 1 est bien le minimum, car :

$$ 1 \leq 2 \\ 1 \leq 3 \\ 1 \leq 4 \\ 1 \leq 6 \\ 1 \leq 9 $$

En revanche, on ne peut pas affirmer que 9 soit le maximum, car les relations (2,9), (4,9) et (6,9) ne sont pas spécifiées :

$$ 1 \leq 9 \\ 3 \leq 9 \\ 2 \; ? \; 9 \\ 4 \; ? \; 9 \\ 6 \; ? \; 9 $$

Il en va de même pour les autres candidats :

4 ne peut pas être le maximum, car on ne sait pas si (4,9), (4,6) ou (4,3) sont vérifiées :

$$ 1 \leq 4 \\ 2 \leq 4 \\ 4 \; ? \; 3 \\ 4 \; ? \; 6 \\ 4 \; ? \; 9 $$

6 n’est pas non plus maximum, car les relations (6,4) et (6,9) restent indéterminées :

$$ 1 \leq 6 \\ 2 \leq 6 \\ 3 \leq 6 \\ 4 \; ? \; 6 \\ 9 \; ? \; 6 $$

Et ainsi de suite.