Ensemble des parties
Qu’appelle-t-on l’ensemble de tous les sous-ensembles ?
L’ensemble des parties, noté \( P(A) \), désigne l’ensemble de tous les sous-ensembles de \( A \), qu’ils soient propres ou impropres. $$ P(A) = \{ S \mid S \subseteq A \} $$ On parle également de puissance d’un ensemble.
Chaque sous-ensemble \( S = \{s_1, \dots\} \) représente une sélection d’éléments de \( A \).
$$ S \subseteq A $$
Ainsi, tout sous-ensemble \( S \) est un élément de l’ensemble des parties \( P(A) \).
$$ S \in P(A) $$
Remarque. Ici, le sous-ensemble est considéré comme un élément parce qu’il appartient à l’ensemble \( P(A) \), d’où l’emploi de la relation d’appartenance \( S \in P(A) \). En revanche, \( S \) est inclus dans \( A \), c’est-à-dire \( S \subseteq A \), et non dans \( P(A) \).
Exemple concret d’ensemble des parties
Soit l’ensemble \( A \) formé des éléments \( a \) et \( b \).
$$ A = \{ a,b \} $$
Les éléments \( a \) et \( b \) appartiennent à \( A \).
$$ a,b \in A $$
Voici le diagramme de Venn correspondant à cet ensemble.
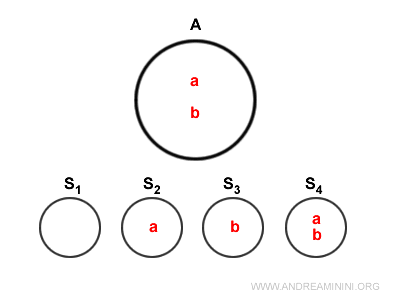
Les sous-ensembles de \( A \) forment l’ensemble des parties \( P(A) \).
$$ \{ \} \\ \{ a \} \\ \{ b \} \\ \{ a,b \} $$
On peut donc écrire :
$$ P(A) = \{ \{ \} , \{ a \} , \{ b \} , \{ a,b \} \} $$
ou, de manière équivalente :
$$ P(A) = \{ ∅ , \{ a \} , \{ b \} , A \} $$
Les ensembles \( \{ a \} \) et \( \{ b \} \) sont des sous-ensembles propres de \( A \).
Tandis que \( ∅ \) et \( A \) en sont les sous-ensembles impropres.
Remarque. Comme tous ces ensembles appartiennent à \( P(A) \), on peut aussi écrire : $$ ∅ , \{ a \} , \{ b \} , A \in P(A) $$
Voici maintenant le diagramme de Venn représentant l’ensemble des parties \( P(A) \).
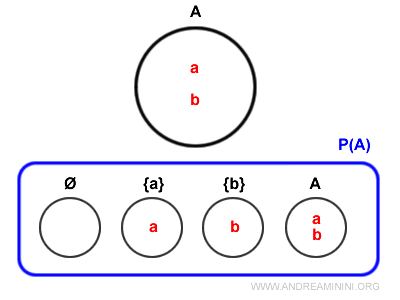
Comme on peut le constater, même l’ensemble \( A \) appartient à \( P(A) \), car tout ensemble est un sous-ensemble impropre de lui-même.
Pourquoi inclut-on aussi l’ensemble vide ?
En théorie des ensembles, l’ensemble vide \( ∅ \) est un sous-ensemble de tout ensemble, sans exception.
Par conséquent, \( ∅ \) est également un sous-ensemble de \( A \),
et fait donc naturellement partie de l’ensemble \( P(A) \).
L’ensemble des parties de l’ensemble vide
Si l’ensemble \( A \) est vide, autrement dit \( A = ∅ \), alors son ensemble des parties est donné par :
$$ P(A) = \{ ∅ \} $$
Il est essentiel de noter que \( \{∅\} \) n’est pas l’ensemble vide, mais un ensemble dont l’unique élément est justement l’ensemble vide.
Pourquoi appelle-t-on cela “ensemble des parties” ?
Cette appellation provient d’une propriété fondamentale.
Si un ensemble \( A \) contient \( n \) éléments, alors son ensemble des parties \( P(A) \) contient exactement \( 2^n \) sous-ensembles.
Exemple
L’ensemble \( A = \{a, b\} \) contient \( n = 2 \) éléments.
Son ensemble des parties compte donc 4 éléments :
$$ 2^n = 2^2 = 4 $$
Et cette règle reste valable pour tout ensemble, quel qu’il soit.