Sous-ensembles

Un ensemble A est un sous-ensemble de B si tous les éléments de A appartiennent également à B.

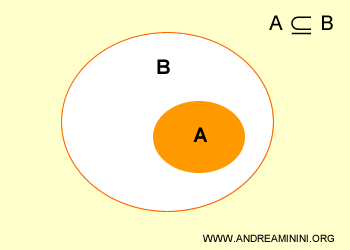
La représentation graphique des ensembles ci-dessus est appelée un diagramme de Venn.

Autrement dit, le sous-ensemble A est contenu dans l’ensemble B.

Cette relation est appelée inclusion.

Pour indiquer une inclusion classique, on utilise le symbole ⊆.

On le lit comme « l’ensemble A est inclus dans l’ensemble B ».

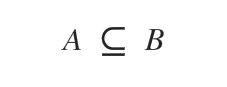
On peut également interpréter cette notation comme « A est un sous-ensemble de B » ou « A est inclus dans B ».

La relation d’inclusion peut aussi être exprimée de cette manière :

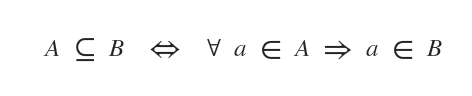
Remarque. La relation d’inclusion couvre aussi le cas où A et B sont identiques, c’est-à-dire qu’ils contiennent exactement les mêmes éléments. Le symbole utilisé combine d’ailleurs celui de l’inclusion (⊂) et celui de l’égalité (=).

Le Sous-ensemble Propre

Un sous-ensemble propre est un sous-ensemble A contenu dans un ensemble B, mais tel que B contient au moins un élément qui n’appartient pas à A.

En d’autres termes, les deux ensembles sont différents, donc A≠B.

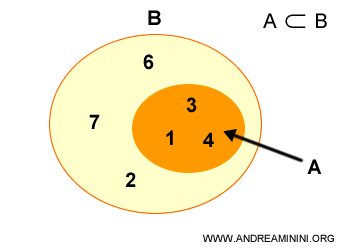
On parle alors d’inclusion stricte.

Il s’agit d’un cas particulier d’inclusion, noté par le symbole ⊂.

On l’interprète comme « l’ensemble A est une partie propre de B ».

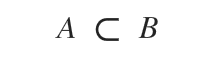
On peut aussi dire que « l’ensemble A est strictement inclus dans l’ensemble B ».

Exemple

L’ensemble A est strictement inclus dans l’ensemble B

$$ A = \{ 1,3,4 \} $$

$$ B = \{ 1,3,4,2,6,7 \} $$

Car tous les éléments de A appartiennent à B, mais B contient d’autres éléments absents de A.

$$ A ⊂ B $$

Quelle est la différence entre inclusion ordinaire et inclusion stricte ? Dans une inclusion stricte (A⊂B), les ensembles A et B sont forcément différents (A≠B). En revanche, une inclusion ordinaire (A⊆B) autorise les deux ensembles à être identiques (A=B). Cela signifie que si l’inclusion stricte A⊂B est vraie, alors l’inclusion ordinaire A⊆B l’est aussi. $$ A⊂B \Longrightarrow A⊆B $$ Mais la réciproque n’est pas forcément vraie, car les ensembles pourraient être égaux (A=B).

Le Sous-ensemble Impropre

• Tout ensemble possède toujours deux sous-ensembles impropres :



 
• l’ensemble lui-même
• l’ensemble vide

A] L’ensemble égal à lui-même

Lorsque deux ensembles sont égaux (A=B), chacun est un sous-ensemble de l’autre.

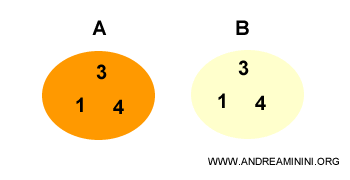
En effet, A contient tous les éléments de B, et B contient tous les éléments de A.

Dans ce cas, on peut dire :

• A est un sous-ensemble impropre de B
• B est un sous-ensemble impropre de A

Cette relation d’implication mutuelle traduit l’égalité des ensembles.

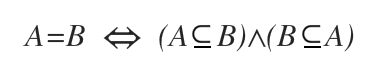
Ainsi, lorsque deux ensembles sont égaux, ils sont aussi des sous-ensembles impropres l’un de l’autre.

Exemple

L’ensemble A est inclus dans B et réciproquement

$$ A = \{ 1,3,4 \} $$

$$ B = \{ 1,3,4 \} $$

Car chaque élément de A appartient à B, et chaque élément de B appartient à A.

Donc, les deux ensembles sont égaux (A=B).

B] L’ensemble vide

L’ensemble vide est considéré comme un sous-ensemble impropre de tout ensemble.

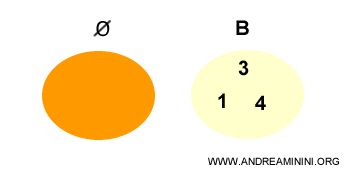
Un ensemble vide est défini comme un ensemble ne contenant aucun élément.

Il est représenté par le symbole Ø. $$ Ø = \{ \ \ \} $$

Remarque. L’idée que l’ensemble vide soit un sous-ensemble de tous les autres ensembles peut sembler contre-intuitive au début, mais elle peut se démontrer (voir démonstration).

Exemple

Considérons l’ensemble vide et un ensemble quelconque A.

$$ Ø = \{ \ \ \} $$

$$ A = \{ 1,3,4 \} $$

L’ensemble vide Ø est aussi strictement inclus dans A

$$ Ø ⊂ A $$

Car on ne peut pas affirmer le contraire.

Démonstration. Cette démonstration se fait par l’absurde. Supposons que l’ensemble vide NE soit PAS un sous-ensemble de A. Cela signifierait qu’il existe au moins un élément de l’ensemble vide qui n’appartient pas à A. Or, c’est impossible puisque l’ensemble vide ne contient aucun élément. Ainsi, si l’affirmation « l’ensemble vide n’est pas un sous-ensemble de A » est fausse, alors l’affirmation contraire « l’ensemble vide est un sous-ensemble de A » est vraie. Autre démonstration. L’union d’un ensemble A avec l’un de ses sous-ensembles B⊆A est toujours égale à A lui-même. $$ A \cup B = A $$ Il en va de même pour l’union d’un ensemble et de l’ensemble vide : $$ A \cup Ø = \{ 1,3,4 \} \cup \{ \ \ \} = \{ 1,3,4 \} = A $$

Le Singleton

Qu’est-ce qu’un singleton ?

Un singleton est un sous-ensemble qui ne contient qu’un seul élément.

Exemple

Le sous-ensemble B est un singleton car c’est un sous-ensemble ( B⊂A ) qui contient un seul élément.

$$ A = \{ 1, 2, 3, 4, 5\} $$

$$ B = \{ 2 \} $$

La Différence Entre Inclusion et Appartenance

Il est important de ne pas confondre inclusion et appartenance.

• La relation d’inclusion ⊆ s’emploie uniquement entre ensembles. Elle permet d’indiquer que A est un sous-ensemble de B. $$ A \subseteq B $$
• La relation d’appartenance ∈ s’applique seulement entre un élément et un ensemble. Elle indique qu’un ou plusieurs éléments, comme a ou b, appartiennent à l’ensemble A. $$ a \in A $$

Remarque : Le même raisonnement vaut pour les relations de non-inclusion et de non-appartenance (∉). $$ a \notin A \\ A \nsubseteq B $$