La différence symétrique entre ensembles

La différence symétrique entre deux ensembles A et B désigne l’ensemble des éléments qui appartiennent à l’un des deux ensembles, mais pas aux deux à la fois. Elle s’exprime ainsi : $$ A \Delta B = (A \setminus B) \cup (B \setminus A) $$

Cette opération permet d’isoler les éléments propres à chaque ensemble, en excluant ceux qui leur sont communs.

La définition formelle est la suivante :

$$ A \Delta B = (A \setminus B) \cup (B \setminus A) $$

Où :

• A\B est l’ensemble des éléments présents dans A mais absents de B.
• B\A est l’ensemble des éléments présents dans B mais absents de A.

Autrement dit, la différence symétrique correspond à l’union des éléments exclusifs à chaque ensemble.

Elle s’avère particulièrement utile lorsqu’on souhaite mettre en évidence les distinctions entre deux ensembles.

Dans un diagramme de Venn, la différence symétrique correspond aux zones non partagées des deux cercles représentant les ensembles.

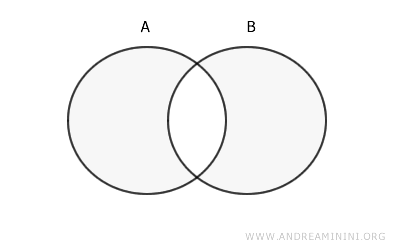
Exemple Concret

Soient les ensembles A et B suivants :

$$ A = \{1, 2, 3\} $$

$$ B = \{2, 3, 4\} $$

Pour déterminer la différence symétrique \(A \Delta B\), on identifie les éléments qui appartiennent uniquement à l’un des deux ensembles :

$$ A \setminus B = \{1\} $$

$$ B \setminus A = \{4\} $$

La différence symétrique est donc :

$$ A \Delta B = \{1\} \cup \{4\} = \{1, 4\} $$

Voici sa représentation dans un diagramme de Venn :

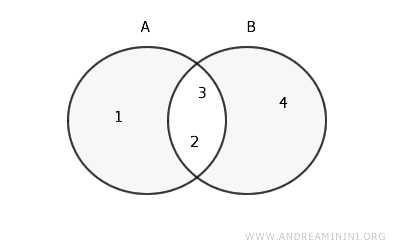
Exemple 2

Considérons maintenant :

$$ A = \{a, b, c\} $$

$$ B = \{c, d, e\} $$

On applique la même démarche :

$$ A \setminus B = \{a, b\} $$

$$ B \setminus A = \{d, e\} $$

La différence symétrique entre A et B est donc :

$$ A \Delta B = \{a, b\} \cup \{d, e\} = \{a, b, d, e\} $$

Dans un diagramme de Venn, cela se représente ainsi :

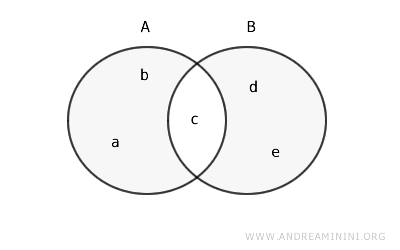
Propriétés de la Différence Symétrique

La différence symétrique possède plusieurs propriétés fondamentales :

• Commutativité
  L’ordre des ensembles n’a aucune incidence sur le résultat : \[ A \Delta B = B \Delta A \]
• Associativité
  Le regroupement des opérations ne modifie pas l’ensemble obtenu : \[ A \Delta (B \Delta C) = (A \Delta B) \Delta C \]
• Élément neutre
  La différence symétrique entre un ensemble et l’ensemble vide donne l’ensemble lui-même : \[ A \Delta \emptyset = A \]
• Idempotence
  La différence symétrique d’un ensemble avec lui-même est toujours l’ensemble vide : \[ A \Delta A = \emptyset \]

Ces propriétés font de la différence symétrique une opération précieuse dans de nombreux domaines des mathématiques.