Partition d’un ensemble

partition P(A)

aucun des sous-ensembles n’est un ensemble vide
l’union de tous les sous-ensembles est égale à A
les sous-ensembles sont mutuellement disjoints, c’est-à-dire qu’ils ne partagent aucun élément

Diviser un ensemble en deux sous-ensembles est ce qu’on appelle une bipartition.

S’il est divisé en trois sous-ensembles, on parle alors de tripartition.

De façon générale, une partition en k sous-ensembles est appelée une k-partition.

Remarque : Il n’existe pas une unique manière de partitionner un ensemble. Un ensemble de k éléments peut être partitionné de k ! façons différentes.

Un exemple concret
Calcul du nombre de partitions
Remarques

Un exemple concret

Considérons l’ensemble fini A composé de 5 éléments :

$$ A = \{ 1,2,3,4,5 \} $$

Voici un exemple de bipartition :

$$ P(A) = \{ \ \{ 1,2,3 \} \ , \ \{ 4,5 \} \ \} $$

Représentée à l’aide d’un diagramme d’Euler-Venn, cette bipartition s’illustre ainsi :

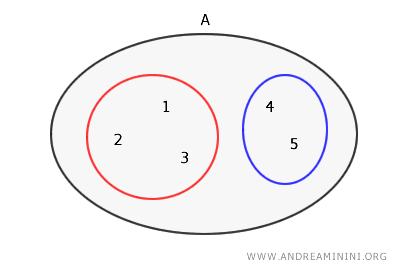
ejemplo de bipartición

Vérification : La partition est composée de deux sous-ensembles non vides, {1,2,3} et {4,5}, qui sont disjoints : $$ \{ 1,2,3 \} \cap \{4,5 \} = Ø $$ Leur union reconstitue l’ensemble A : $$ \{ 1,2,3 \} \cup \{4,5 \} = \{ 1,2,3,4,5 \} = A $$

Comme A contient 5 éléments, il existe 52 partitions possibles.

Par exemple, une autre bipartition est :

$$ P(A) = \{ \ \{ 1,2 \} \ , \ \{ 3,4,5 \} \ \} $$

On peut également former la tripartition suivante :

$$ P(A) = \{ \ \{ 1,2 \} \ , \ \{ 3,4 \} \ , \ \{ 5 \} \ \} $$

Ou encore diviser A en 4 sous-ensembles :

$$ P(A) = \{ \ \{ 1,2 \} \ , \ \{ 3 \} \ , \ \{ 4 \} \ , \ \{ 5 \} \ \} $$

En tout, il y a 52 façons distinctes de partitionner les éléments de A.

Calcul du nombre de partitions

Le nombre de partitions d’un ensemble fini $ A $ comportant $ n $ éléments est donné par le nombre de Bell $ B_n $, que l’on peut calculer à l’aide de la formule récursive suivante, avec la condition initiale $ B_0 = 1 $ :

$$ B_n = \sum_{k=0}^{n-1} \binom{n-1}{k} B_k $$

Dans cette formule :

$ \binom{n-1}{k} $ est un coefficient binomial indiquant de combien de façons on peut choisir $ k $ éléments parmi $ n-1 $
$ B_k $ représente le nombre de Bell correspondant à un ensemble de $ k $ éléments

Le nombre de Bell $ B_n $ donne donc le nombre total de partitions possibles d’un ensemble de $ n $ éléments en sous-ensembles disjoints.

Il peut aussi être déterminé par la formule exponentielle de Dobinski :

$$ B_n = \frac{1}{e} \sum_{k=0}^{\infty} \frac{k^n}{k!} $$

Mais en pratique, c’est la formule récursive qui est la plus utilisée. Par exemple, elle permet de calculer $ B_5 = 52 $ pour l’ensemble $ A = \{1,2,3,4,5\} $.

Exemple

Calculons le nombre de partitions de l’ensemble $ A $, où $ n = 5 $ :

$$ A = \{ 1,2,3,4,5 \} $$

On applique la formule :

$$ B_n = \sum_{k=0}^{n-1} \binom{n-1}{k} B_k $$

Dans notre cas :

$$ B_5 = \sum_{k=0}^{4} \binom{4}{k} B_k $$

Avec $ B_0 = 1 $ comme point de départ, nous procédons étape par étape.

Calculons d’abord $ B_1 $ :

$$ B_1 = \binom{0}{0} B_0 = 1 \times 1 = 1 $$

Puis $ B_2 $ :

$$ B_2 = \binom{1}{0} B_0 + \binom{1}{1} B_1 = 1 + 1 = 2 $$

Ensuite $ B_3 $ :

$$ B_3 = \binom{2}{0} B_0 + \binom{2}{1} B_1 + \binom{2}{2} B_2 = 1 + 2 + 2 = 5 $$

Calculons maintenant $ B_4 $ :

$$ B_4 = \binom{3}{0} B_0 + \binom{3}{1} B_1 + \binom{3}{2} B_2 + \binom{3}{3} B_3 = 1 + 3 + 6 + 5 = 15 $$

Enfin, calculons $ B_5 $ :

$$ B_5 = \binom{4}{0} B_0 + \binom{4}{1} B_1 + \binom{4}{2} B_2 + \binom{4}{3} B_3 + \binom{4}{4} B_4 = 1 + 4 + 12 + 20 + 15 = 52 $$

On obtient donc $ B_5 = 52 $.

En conclusion, il existe 52 partitions distinctes de l’ensemble $ A = \{ 1,2,3,4,5 \} $. Ce résultat est obtenu à l’aide de la formule récursive et des coefficients binomiaux.

Remarques

La partition triviale
Tout ensemble X admet une partition triviale constituée uniquement de lui-même : $$ P(A) = \{ A \} $$
Exemple : Pour l’ensemble $$ A = \{ 1,2,3,4,5 \} $$ la partition triviale est : $$ P(A) = \{ \ \{ 1,2,3,4,5 \} \ \} $$
La partition en singletons
Il est également possible de partitionner un ensemble en sous-ensembles à un seul élément (appelés singletons) : $$ P(A) = \{ \{ a_1 \} , \{ a_2 \} , ... \} $$
Exemple : Pour l’ensemble $$ A = \{ 1,2,3,4,5 \} $$ la partition en singletons est : $$ P(A) = \{ \ \{ 1 \} \ , \{ 2 \} \ , \{ 3 \} \ , \{ 4 \} \ , \{ 5 \} \ \} $$

Et ainsi de suite.