Complément d’un Ensemble

En théorie des ensembles, si B est un sous-ensemble de A $$ B⊆A $$ le complément relatif de B par rapport à A est l’ensemble des éléments de A qui n’appartiennent pas à B. $$ A \text{ \ } B = \{ x \in A \mid x \notin B \} $$ On parle aussi du complément relatif de B dans A.

Cette expression se lit : « l’ensemble A\B est le complément de B » ou « le complément relatif de B dans A ».

Le diagramme de Venn ci-dessous en illustre la représentation graphique :

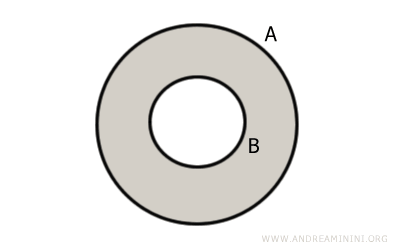
La zone grisée correspond au complément de B dans A, c’est-à-dire l’ensemble A\B.

Ce complément coïncide avec la différence entre ensembles A - B.

Exemple concret

Considérons deux ensembles finis A et B :

$$ A = \{ 2, 4, 6, 8, 10 \} $$

$$ B = \{ 4, 6 \} $$

Le complément de B dans A est constitué des éléments de A qui n’appartiennent pas à B :

$$ A \text{ \ } B = A - B = \{ 2, 8, 10 \} $$

Voici sa représentation à l’aide d’un diagramme d’Euler-Venn :

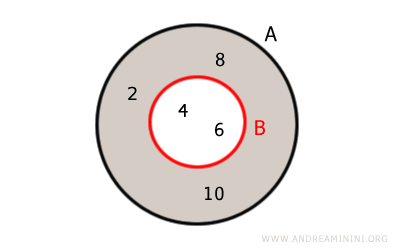
Explication. Les éléments 4 et 6 sont présents à la fois dans A et dans B, donc ils ne figurent pas dans le complément. Le complément de B dans A est l’ensemble des éléments de A qui ne sont pas dans B, soit {2, 8, 10}.

Exemple 2

Examinons à présent le cas de deux ensembles infinis.

L’ensemble des entiers naturels \( N = \{1, 2, 3, 4, 5, ...\} \) et le sous-ensemble des naturels pairs \( P = \{2, 4, 6, 8, ...\} \).

$$ N = \{ 1, 2, 3, 4, 5, ... \ \} $$

$$ P = \{ 2, 4, 6, 8, ... \ \} $$

Le complément de P dans N est l’ensemble des entiers naturels impairs, noté \( D \) :

$$ N \text{ \ } P = D = \{ 1, 3, 5, 7, 9, ... \ \} $$

Complément Absolu

Le complément absolu d’un ensemble A, par rapport à l’ensemble universel U, est l’ensemble de tous les éléments de U qui ne sont pas dans A : $$ C_A = \{ x \in U \mid x \notin A \} $$ On parle aussi du complément absolu de A.

Qu’appelle-t-on ensemble universel ?

L’ensemble universel \( U \) est l’ensemble qui contient tous les éléments pertinents dans un cadre donné.

Sauf indication contraire, on considère que U regroupe tous les objets possibles de l’univers d’étude.

Exemple

Soit un ensemble \( A \) inclus dans un ensemble universel \( U \).

Le complément de \( A \), noté \( C_A \), est l’ensemble des éléments de \( U \) qui ne figurent pas dans \( A \). Sur le diagramme, la zone grisée représente \( C_A \), tandis que la zone blanche correspond à \( A \).

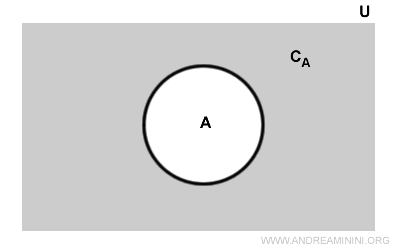
On dira alors que : « l’ensemble U\A (ou U-A) est le complément de A ».

Ce complément peut aussi s’écrire \( U - A \), \( C_A \), \( A^C \) ou encore \( -A \).

Remarques

Voici quelques propriétés fondamentales des compléments :

• Le complément de A par rapport à lui-même est l’ensemble vide :

  $$ A \text{ \ } A = A - A = \Oslash $$

• Si \( A = B \), alors leur différence est vide :

  $$ A = B \Longleftrightarrow A - B = \Oslash $$

• Le complément de l’ensemble vide dans A est A lui-même :

  $$ \Oslash \text{ \ } A = A $$

• L’union de A avec son complément dans B restitue l’ensemble B :

  $$ A \cup (B \text{ \ } A) = B $$

• L’intersection de A avec son complément dans B est vide :

  $$ A \cap (B \text{ \ } A) = \Oslash $$

Et ainsi de suite.