Union d’Ensembles

L’union de deux ensembles A et B est l’ensemble constitué de tous les éléments appartenant soit à A, soit à B, soit aux deux.

Le symbole utilisé pour représenter l’union est ∪.

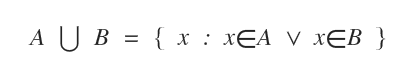
On lit cette expression comme union de A et B, ou plus simplement A union B.

Lorsque des éléments sont communs aux deux ensembles, ils ne figurent qu’une seule fois dans l’union.

Union de plusieurs ensembles. L’union peut également être étendue à une collection de plusieurs ensembles. On la note de la manière suivante : $$ \bigcup_{i \in I} = \{ x \in A_i \:\: \text{pour un certain}\:\: i \in I \} $$

Exemple concret

Supposons que nous ayons deux ensembles A et B.

L’ensemble A contient les éléments { 2, 5, 6, 7, 8 }, tandis que B est formé des éléments { 1, 3, 4, 6, 7, 9 }.

L’union de A et B, notée A ∪ B, est l’ensemble { 1, 2, 3, 4, 5, 6, 7, 8, 9 }.

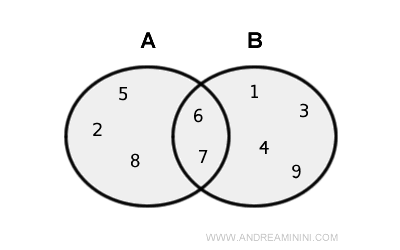
Remarque. Les éléments {6, 7} apparaissent à la fois dans A et dans B. Toutefois, ils ne sont inclus qu’une seule fois dans A ∪ B, car un ensemble ne contient jamais de doublons.

Exemple 2

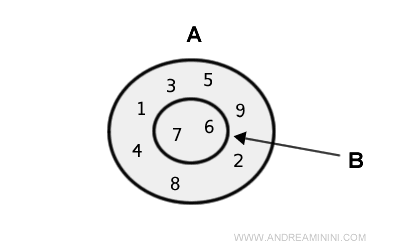
Considérons les ensembles suivants :

$$ A = \{ 1 , 2, 3, 4, 5, 6, 7, 8, 9 \} $$

$$ B = \{ 2, 4, 6, 8 \} $$

Ici, B est un sous-ensemble propre de A.

Dans ce cas, leur union est simplement égale à A :

$$ A \cup B = \{ 1 , 2, 3, 4, 5, 6, 7, 8, 9 \} $$

Les éléments communs ne sont jamais dupliqués dans l’union.

Exemple 3

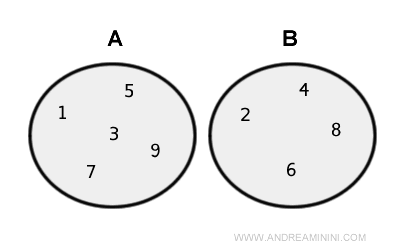
Considérons maintenant les ensembles suivants :

$$ A = \{ 1 , 3, 5, 7, 9 \} $$

$$ B = \{ 2, 4, 6, 8 \} $$

Ces deux ensembles sont disjoints, c’est-à-dire qu’ils ne possèdent aucun élément en commun.

Leur union regroupe donc tous les éléments de A et de B :

$$ A \cup B = \{ 1 , 2, 3, 4, 5, 6, 7, 8, 9 \} $$

Le diagramme suivant illustre cette union à l’aide de représentations de type Euler-Venn.

Remarque. L’union d’ensembles fonctionne comme la disjonction logique inclusive (“OU”). Contrairement à la disjonction exclusive (XOR), qui élimine les cas de recouvrement, l’union retient tous les éléments appartenant à l’un ou à l’autre ensemble, y compris ceux qu’ils ont en commun.

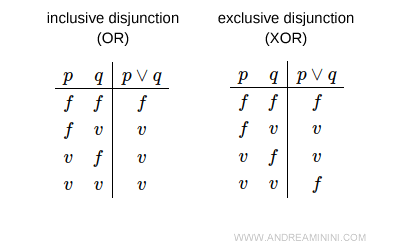
C’est pourquoi, lorsqu’on établit un parallèle avec la logique, il est essentiel de préciser qu’il s’agit bien de la disjonction inclusive.

Propriétés de l’union

L’union d’ensembles possède plusieurs propriétés, analogues à celles de l’addition ou de la multiplication en arithmétique :

• Propriété commutative
  L’ordre des ensembles n’a pas d’effet sur le résultat : $$ A \cup B = B \cup A $$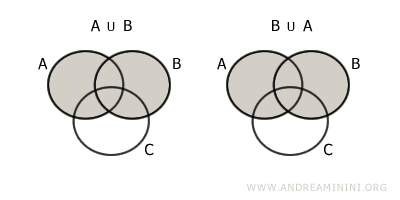

  

• Propriété associative
  Le regroupement des ensembles n’influence pas l’union : $$ (A \cup B) \cup C = A \cup (B \cup C) $$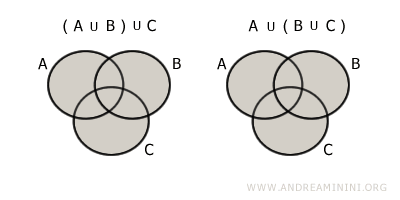

  

• Distributivité de l’union sur l’intersection
  L’union d’un ensemble avec l’intersection de deux autres équivaut à l’intersection de leurs unions respectives :

  $$ A \cup (B \cap C) = (A \cup B) \cap (A \cup C) $$
  

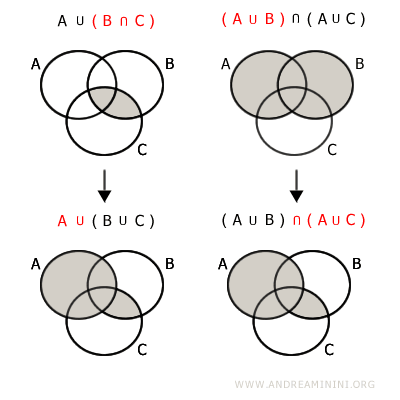
Cardinalité de l’union

La cardinalité d’une union dépend de la présence ou non d’éléments partagés entre les ensembles concernés.

• Ensembles disjoints
  Lorsqu’aucun élément n’est commun, la cardinalité de l’union est simplement la somme des cardinalités : $$ |A\cup B| = |A| + |B| $$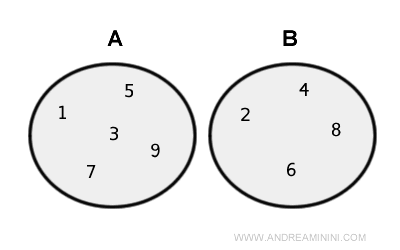

  

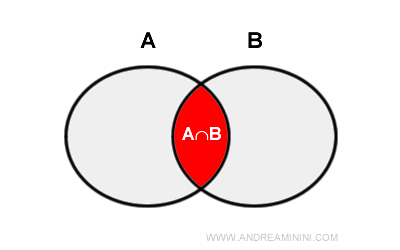
• Ensembles avec des éléments en commun
  Si les ensembles partagent des éléments, on retire la cardinalité de leur intersection pour éviter les doublons : $$ |A\cup B| = |A| + |B| - |A\cap B| $$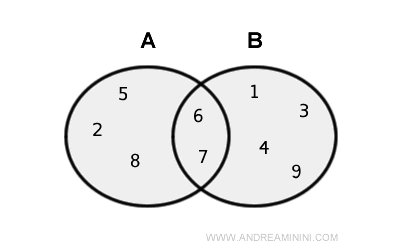

  

  Explication. Lorsque l’on additionne les éléments de A et de B, ceux de l’intersection A ∩ B sont comptés deux fois. Il faut donc les soustraire une fois pour obtenir la cardinalité exacte de A ∪ B.

  

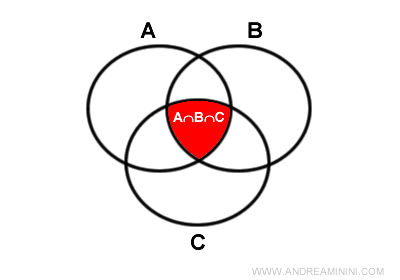
  Dans le cas de trois ensembles non disjoints, on applique le principe d’inclusion-exclusion :

  $$ |A\cup B\cup C| = |A| + |B| + |C| - |A\cap B| - |A\cap C| - |B\cap C| + |A\cap B\cap C| $$

  Les intersections deux à deux sont retranchées pour éviter les comptages doubles, mais l’intersection des trois ensembles est alors supprimée à l’excès : il faut donc la réintroduire une fois.

  Explication. En additionnant |A|, |B| et |C|, les éléments communs à deux ensembles sont comptés deux fois, et ceux appartenant aux trois ensembles le sont trois fois. Pour corriger cela, on soustrait chaque intersection binaire une fois, puis on rajoute l’intersection triple pour rétablir le bon compte.
  

Ce principe s’étend naturellement à l’union de plus de trois ensembles, toujours selon la même logique d’inclusion-exclusion.