Ensembles Bornés
Qu’est-ce qu’un ensemble borné ?
Un ensemble est dit borné s’il existe un réel \( M \) tel que tous ses éléments soient compris entre \( -M \) et \( +M \). Autrement dit : $$ -M \leq a \leq M \quad \forall \: a \in A $$ ou, de manière équivalente : $$ |a| \leq M \quad \forall \: a \in A $$
Un ensemble borné est donc à la fois majoré et minoré.
Démonstration
A] Supposons que :
$$ |a| \leq M \quad \forall \: a \in A $$
D’après la définition de la valeur absolue, on déduit immédiatement :
$$ -M \leq a \leq M \quad \forall \: a \in A $$
Ainsi, \( -M \) constitue une borne inférieure et \( M \) une borne supérieure de l’ensemble.
B] Inversement, supposons que :
$$ l \leq a \leq L \quad \forall \: a \in A $$
avec \( l \) et \( L \) deux réels. Pour exprimer cette double inégalité sous la forme \( |a| \leq M \), on définit :
$$ M = \max(|l|, |L|) $$
ce qui permet d’écrire :
$$ |a| \leq M \quad \forall \: a \in A $$
et donc :
$$ -M \leq l \leq a \leq L \leq M \quad \forall \: a \in A $$
Exemple concret
Soit l’ensemble réel \( A \) composé des sept éléments suivants :
$$ A = \{ -7, 4, 2, 6, 3, 5, 1 \} $$
Il admet une infinité de bornes inférieures dans \( (-\infty, -7] \) et de bornes supérieures dans \( [6, +\infty) \).
Les bornes optimales sont la plus grande borne inférieure \( l = -7 \) et la plus petite borne supérieure \( L = 6 \).
$$ l = -7, \quad L = 6 $$
On pose alors :
$$ M = \max(|l|, |L|) = \max(7, 6) = 7 $$
Comme il existe un réel \( M = 7 \) tel que :
$$ -M \leq a \leq M \quad \forall a \in A $$
on conclut que l’ensemble \( A \) est borné.
Ensembles minorés
Un ensemble est minoré s’il existe un réel \( M \) tel que tous ses éléments vérifient : $$ a \geq M \quad \forall \: a \in A $$
Tout ensemble minoré admet au moins une borne inférieure.
Dans ce cas, il existe une plus grande de ces bornes inférieures, appelée infimum.
Dans un ensemble non vide et borné, l’infimum est la plus grande de toutes les bornes inférieures :
$$ m = \inf(A) = \begin{cases} m \leq a \quad \forall a \in A \\ \\ \forall \epsilon > 0,\ \exists\ a \in A \ \text{tel que}\ m + \epsilon > a \end{cases} $$
Exemple : L’ensemble \( \mathbb{R}^+ \) des réels positifs est minoré car tous ses éléments sont strictement supérieurs à 0. Son infimum est \( m = 0 \), la plus grande borne inférieure. En revanche, il n’est pas majoré et son supremum est donc \( +\infty \).
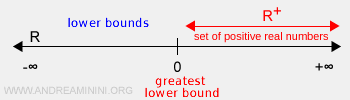
Si un ensemble n’est pas minoré, son infimum est \( -\infty \) :
$$ \inf(A) = -\infty \Leftrightarrow \forall l \in \mathbb{R},\ \exists a \in A \ \text{tel que}\ a < l $$
Ensembles majorés
Un ensemble est majoré s’il existe un réel \( M \) tel que : $$ a \leq M \quad \forall \: a \in A $$
Tout ensemble majoré admet au moins une borne supérieure.
Il existe alors une plus petite de ces bornes, appelée supremum.
Dans un ensemble non vide et borné, le supremum est la plus petite de toutes les bornes supérieures :
$$ M = \sup(A) = \begin{cases} M \geq a \quad \forall a \in A \\ \\ \forall \epsilon > 0,\ \exists\ a \in A \ \text{tel que}\ M - \epsilon < a \end{cases} $$
Exemple : L’ensemble \( \mathbb{R}^- \) des réels négatifs est majoré car tous ses éléments sont strictement inférieurs à 0. Son supremum est \( M = 0 \), la plus petite borne supérieure. Mais comme il n’est pas minoré, son infimum est \( -\infty \).
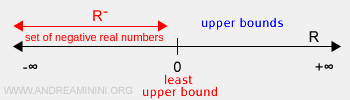
Un ensemble non majoré a pour supremum \( +\infty \) :
$$ \sup(A) = +\infty \Leftrightarrow \forall L \in \mathbb{R},\ \exists a \in A \ \text{tel que}\ a > L $$
Ensemble borné dans le plan
Un ensemble \( A \subseteq \mathbb{R}^2 \) est dit borné s’il existe un réel \( M > 0 \) et un point \( P_0 \in \mathbb{R}^2 \) tels que la distance entre tout point \( P \in A \) et \( P_0 \) soit strictement inférieure à \( M \) : \[ \exists\ P_0 \in \mathbb{R}^2,\ \exists\ M > 0 \ \text{tel que}\ \forall\ P \in A,\quad d(P, P_0) < M \] où \( d(P, P_0) \) désigne la distance euclidienne.
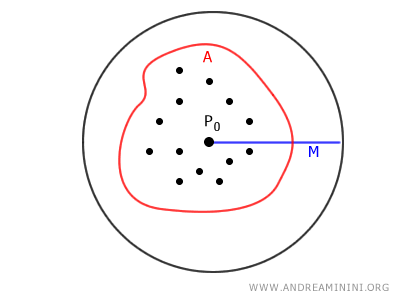
Autrement dit, un ensemble du plan est borné si tous ses points sont contenus dans un disque de rayon fini.
De façon générale, un ensemble est borné s’il ne s’étend pas à l’infini dans aucune direction et s’il peut être entièrement inclus dans un cercle suffisamment grand.
Exemples d’ensembles bornés dans \( \mathbb{R}^2 \) :
- Un disque de rayon \( r \), avec ou sans son bord.
- Un carré, un rectangle, un triangle ou tout autre polygone fermé.
- Toute figure fermée de dimensions finies.
Remarque : À l’inverse, sont non bornés une droite, une parabole, une spirale qui s’éloigne indéfiniment comme \( y = x^2 \), ou encore un quadrant entier du plan cartésien.