Différence entre ensembles ouverts et fermés

Les notions d’ensembles ouverts et fermés sont fondamentales pour appréhender la structure des espaces topologiques. La différence essentielle tient à la présence ou non des points de frontière dans l’ensemble.

Un ensemble fermé contient tous ses points de frontière, tandis qu’un ensemble ouvert les exclut.

Autrement dit, les points de la frontière font partie d’un ensemble fermé, alors qu’ils sont extérieurs à un ensemble ouvert.

Voyons à présent ces deux concepts plus en détail :

Ensemble ouvert
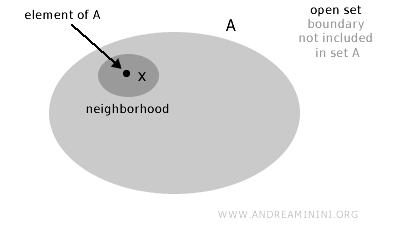
Un ensemble ouvert est un ensemble qui ne contient aucun de ses points de frontière.
Plus rigoureusement, un ensemble \(A\) d’un espace topologique \(X\) est dit ouvert si, pour tout point \(x \in A\), il existe un voisinage entièrement inclus dans \(A\). Autrement dit, autour de chaque point de l’ensemble, on peut tracer un « voisinage » qui reste complètement à l’intérieur de l’ensemble, sans toucher la frontière.

Exemple. Un exemple simple d’ensemble ouvert est l’intervalle \( (3,10) \) dans les réels. Il comprend tous les nombres \( x \) tels que \( 3 < x < 10 \), mais exclut les bornes 3 et 10. Ces valeurs ne faisant pas partie de l’intervalle, cet exemple illustre parfaitement ce qu’est un ensemble ouvert en une dimension.
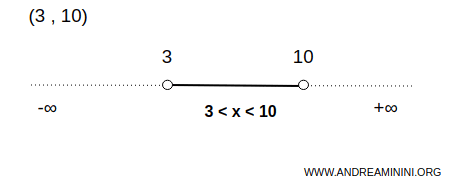
Ensemble fermé
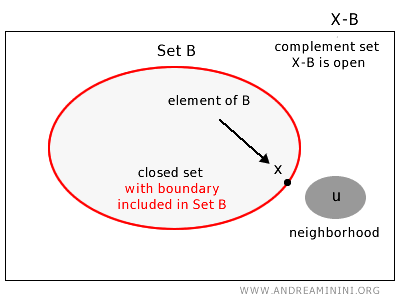
Un ensemble fermé est un ensemble qui contient l’intégralité de ses points de frontière.
Formellement, un ensemble \(B\) d’un espace topologique \(X\) est fermé si son complémentaire dans \(X\), c’est-à-dire l’ensemble des points \(u \in X\) n’appartenant pas à \(B\), est un ensemble ouvert. Une autre caractéristique essentielle des ensembles fermés est qu’ils contiennent tous leurs points d’adhérence.

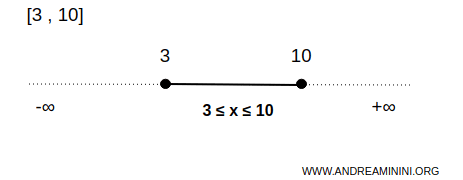
Exemple. Reprenons le cas de l’intervalle réel. L’intervalle fermé \( [3,10] \) contient tous les réels \( x \) tels que \( 3 \leq x \leq 10 \), y compris les extrémités 3 et 10. Contrairement à l’intervalle ouvert, ces bornes appartiennent à l’ensemble. Ainsi, tout voisinage de ces points contient des éléments de \( B \). Par exemple, l’intervalle centré en 3 de rayon \( 0{,}01 \), soit \( [2{,}99, 3{,}01] \), contient des points extérieurs à \( B \), ce qui montre que 3 est bien un point de frontière - inclus dans l’ensemble. Cet exemple est emblématique d’un ensemble fermé en une dimension.

Pourquoi est-il crucial de distinguer ensembles ouverts et fermés ?

La distinction entre ensembles ouverts et fermés est au cœur de nombreuses disciplines mathématiques, telles que l’analyse fonctionnelle, la géométrie différentielle ou encore la théorie des groupes topologiques. Comprendre ces notions permet de décrire finement la structure interne des espaces et de formuler des propriétés fondamentales comme la continuité, la compacité ou la connexité.

Remarques

Quelques précisions complémentaires :

Ensembles clopens et ensembles ni ouverts ni fermés
Dans certains espaces topologiques, un ensemble peut être à la fois ouvert et fermé. On les appelle alors « ensembles clopens ». Il existe également des ensembles qui ne sont ni ouverts ni fermés.
Par exemple, dans tout espace topologique, l’ensemble vide et l’espace tout entier sont systématiquement ouverts et fermés à la fois. Ce sont les exemples les plus élémentaires d’ensembles clopens.

Et ainsi de suite.