Ensembles Fermés

On dit qu’un ensemble $ B $ dans un espace topologique $ X $ est fermé si, pour tout élément du complémentaire $ u \in X - B $, il existe un voisinage entièrement contenu dans ce complémentaire $ X - B $.
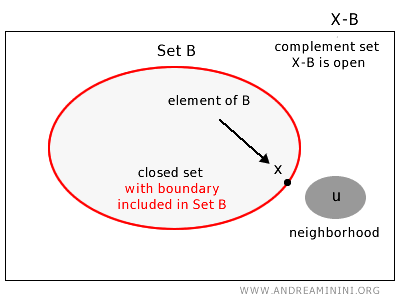
exemple d’un ensemble fermé

Autrement dit, un ensemble est fermé s’il renferme tous ses points frontières.

Plus rigoureusement, un ensemble $ B $ dans un espace topologique $ X $ est fermé si son complémentaire $ X - B $ est un ensemble ouvert.

Remarque : Cela implique que dans $ B $, il existe au moins un point autour duquel aucun voisinage ne peut être entièrement contenu dans $ B $.

Un exemple concret
Le complémentaire d’un ensemble fermé
Exemple
Propriétés des ensembles fermés
Exemple
Remarques supplémentaires

Un exemple concret

Considérons la droite réelle $ \mathbb{R} $ et un intervalle fermé.

Qu’est-ce qu’un intervalle fermé ? Un intervalle fermé dans $ \mathbb{R} $ est l’ensemble des points $ x $ tels que $ a \leq x \leq b $, où $ a $ et $ b $ sont deux nombres réels avec $ a < b $, et où les deux bornes sont incluses.

On note ces intervalles $[a,b]$, les crochets signifiant que les extrémités $ a $ et $ b $ appartiennent à l’ensemble.

Par exemple, l’intervalle fermé $[3,10]$ constitue un ensemble fermé sur la droite réelle $ \mathbb{R} $.

Ici, l’ensemble $ B $ regroupe tous les nombres compris entre 3 et 10, extrémités incluses.

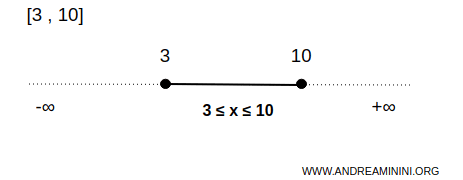
exemple d’un ensemble fermé

En d’autres termes, tout point $ x $ vérifiant $ 3 \leq x \leq 10 $ appartient à cet ensemble, y compris les bornes $ x=3 $ et $ x=10 $.

Cela dit, dans ce cas, tous les points ne possèdent pas nécessairement un voisinage entièrement inclus dans l’intervalle $[3,10]$.

Par exemple, tout voisinage de l’extrémité inférieure $ x=3 $ contiendra forcément des points plus petits que 3, qui ne sont pas dans l’intervalle.

Remarque : Même en choisissant un voisinage infiniment petit, comme $ 3 \pm 0,00000001 $, celui-ci ne serait pas entièrement contenu dans $[3,10]$, car $ 3 - 0,00000001 < 3 $. Il en va de même pour l’extrémité supérieure $ x=10 $, pour laquelle aucun voisinage ne peut être totalement inclus dans l’intervalle.

Voici donc un exemple simple d’ensemble fermé en dimension une.

Autres exemples d’ensembles fermés

On peut étendre la même idée au plan ($\mathbb{R}^2$).

Considérons, par exemple, l’ensemble des points à l’intérieur d’un disque de rayon $ r=1 $ centré en $(0,0)$ :

$$ x^2 + y^2 \leq 1 $$

Cette inégalité décrit tous les points dont la distance au centre $(0,0)$ est inférieure ou égale à 1, englobant à la fois l’intérieur du disque et les points de la circonférence.

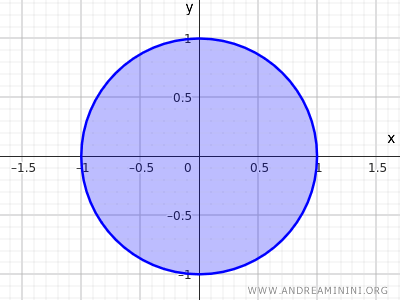
exemple d’un ensemble fermé dans le plan

Il s’agit là d’un autre exemple d’ensemble fermé.

Comme on peut le constater, les points situés sur la circonférence $ x^2 + y^2 = 1 $ ne disposent pas de voisinages entièrement contenus dans le disque fermé.

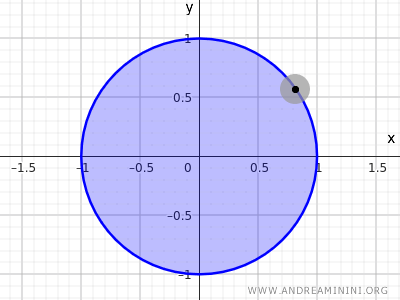
exemple d’un ensemble fermé

Remarque : En topologie, la circonférence définie par l’équation $ x^2 + y^2 = 1 $ n’est ni un ensemble ouvert ni un ensemble fermé dans l’espace euclidien $ \mathbb{R}^2 $, puisqu’elle comprend uniquement les points du cercle et exclut son intérieur. En revanche, l’ensemble défini par $ x^2 + y^2 \leq 1 $, incluant à la fois les points à l’intérieur et ceux sur la circonférence, est un exemple typique d’ensemble fermé, car il contient tous ses points frontières.

De façon analogue, la notion d’ensemble fermé s’étend à l’espace tridimensionnel avec une sphère pleine, et même à l’espace $ n $-dimensionnel avec une $ n $-sphère fermée.

Le complémentaire d’un ensemble fermé

Dans un espace topologique $ X $, le complémentaire d’un ensemble fermé $ C $ est un ensemble ouvert, noté $ X - C $.

En d’autres termes, si $ C $ est fermé dans $ X $, alors son complémentaire $ X - C $ est nécessairement ouvert.

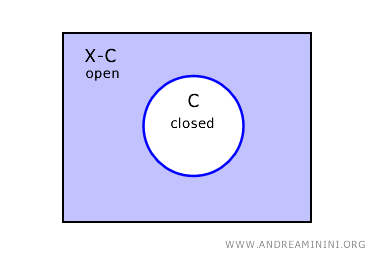
Le complémentaire d’un ensemble fermé

Réciproquement, si un ensemble $ U $ est ouvert, son complémentaire $ X - U $ est fermé dans $ X $.

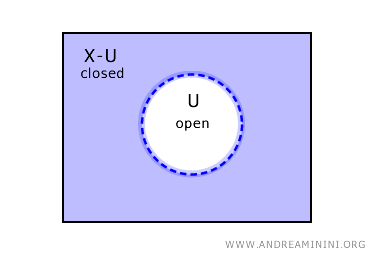
Le complémentaire d’un ensemble ouvert

Cependant, ce ne sont pas les seules possibilités. Dans certains espaces topologiques, il existe des ensembles qui sont à la fois ouverts et fermés, ainsi que des ensembles qui ne sont ni ouverts ni fermés.

Autrement dit, le fait qu’un ensemble ne soit pas fermé n’implique pas nécessairement qu’il soit ouvert, et inversement, un ensemble non ouvert n’est pas forcément fermé.

Exemple

Considérons un espace topologique $ (X, T) $, où l’ensemble $ X = \{a,b,c,d\} $ comprend quatre éléments, et où la topologie $ T $ est donnée par les ensembles ouverts suivants :

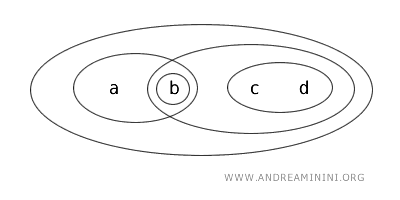
Exemple

Les ensembles ouverts de cette topologie sont : $ \{b\}, \{a,b\}, \{c,d\}, \{b,c,d\}, X $ et l’ensemble vide $ \varnothing $.

Voyons quelques cas particuliers :

L’ensemble $ \{b\} $ est ouvert, car il est explicitement défini comme tel dans la topologie.
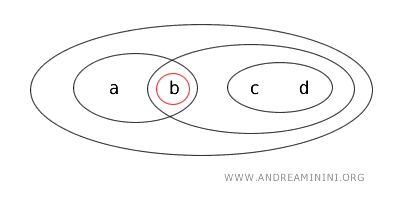
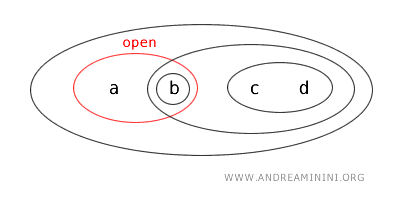
L’ensemble $ \{a\} $ est fermé, car son complémentaire est un ensemble ouvert dans cette topologie. En effet, $ X - \{a\} = \{b,c,d\} $ est ouvert.
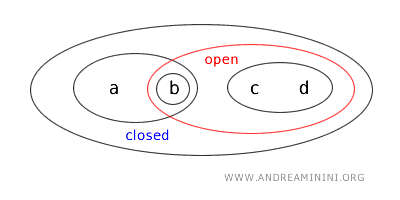
L’ensemble $ \{a,b\} $ est à la fois ouvert et fermé (clopen). Bien que cela soit rare dans les topologies classiques sur $ \mathbb{R} $, dans des espaces plus généraux, un ensemble peut être simultanément ouvert et fermé si son complémentaire est également ouvert. Ici, $ \{a,b\} $ est ouvert par définition de la topologie et, de plus, son complémentaire $ X - \{a,b\} = \{c,d\} $ est ouvert, ce qui en fait aussi un ensemble fermé.
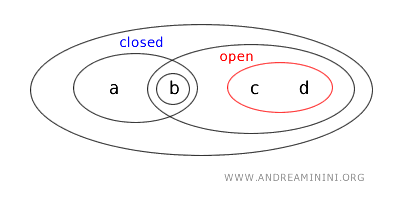
L’ensemble $ \{b,c\} $ n’est ni ouvert ni fermé. Il n’apparaît pas dans la liste des ensembles ouverts de la topologie, et son complémentaire $ X - \{b,c\} = \{a,d\} $ n’est pas non plus un ensemble ouvert. Il ne remplit donc pas les critères ni d’ouverture ni de fermeture.

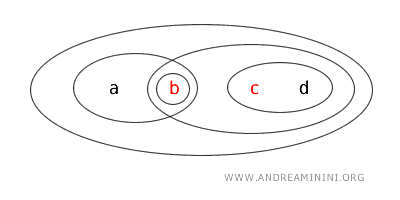
Cet exemple montre bien qu’un ensemble dans un espace topologique peut être ouvert, fermé, les deux à la fois (clopen), ou ni l’un ni l’autre.

Propriétés des ensembles fermés

Un ensemble fermé se définit comme le complémentaire d’un ensemble ouvert. Parmi ses principales propriétés, on trouve :

L’ensemble vide ($\varnothing$) et l’espace tout entier $ X $ sont toujours des ensembles fermés.
L’intersection de toute collection (finie ou infinie) d’ensembles fermés est elle-même un ensemble fermé.
L’union d’un nombre fini d’ensembles fermés reste un ensemble fermé.

Exemple

Dans la topologie usuelle de l’espace euclidien $ \mathbb{R}^n $, tout point isolé constitue un ensemble fermé.

Si l’on prend un point $ n $ sur la droite réelle ($ \mathbb{R}^1 $), son complémentaire est l’ensemble de tous les points de $ \mathbb{R}^1 $ sauf $ n $.

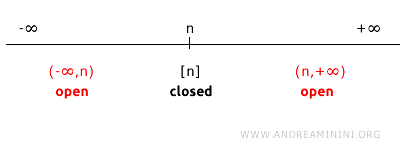
Exemple

Le complémentaire de $\{n\}$ est l’union de deux intervalles ouverts : $(-\infty, n) \cup (n, +\infty)$.

Comme les intervalles $(-\infty, n)$ et $(n, +\infty)$ sont ouverts dans la topologie usuelle, leur union $(-\infty, n) \cup (n, +\infty)$ forme également un ensemble ouvert.

On en conclut donc que $\{n\}$ est un ensemble fermé, puisque son complémentaire est ouvert.

Cela dit, dans toutes les topologies, les points isolés ne constituent pas nécessairement des ensembles fermés. Cela dépend de la structure topologique de l’espace considéré.

Considérons une topologie sur $ \mathbb{R} $, engendrée par les intervalles ouverts $ (n, n+1) $, pour chaque entier $ n $. Dans cette topologie, les points isolés $ n $ ne sont pas des ensembles fermés, car ils ne peuvent pas s’exprimer comme le complémentaire d’un ensemble ouvert.
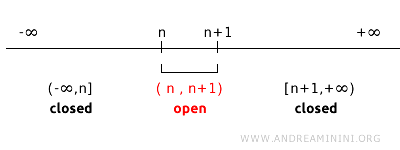
Exemple
Par exemple, les ensembles $ (1,2) $ et $ (2,3) $ sont ouverts dans cette topologie. Le complémentaire de l’ensemble ouvert $ (1,2) $ est $ (-\infty, 1] \cup [2, +\infty) $, tandis que celui de $ (2,3) $ est $ (-\infty, 2] \cup [3, +\infty) $.

Dans cette topologie, il est impossible de trouver un ensemble ouvert dont le complémentaire soit exactement $\{2\}$. De façon générale, pour tout ensemble ouvert de la forme $ (n, n+1) $, son complémentaire est une union d’intervalles fermés $ (-\infty, n] \cup [n+1, +\infty) $. Ainsi, dans cette topologie, les points isolés $ n $ ne sont pas fermés, ce qui montre que la notion d’ensemble fermé dépend étroitement de la topologie choisie.

Remarques supplémentaires

Voici quelques précisions intéressantes :

Ensembles fermés et points d’accumulation
Un point d’accumulation d’un ensemble est un point dont tout voisinage, si petit soit-il, contient toujours au moins un autre point de cet ensemble. Cette propriété est caractéristique des ensembles fermés, car un ensemble est fermé s’il renferme tous ses points d’accumulation.

Exemple : Prenons l’intervalle fermé $[0,1]$ sur la droite réelle. Cet ensemble contient tous ses points d’accumulation.

Par exemple, le point $0,5$ dans $[0,1]$ possède tout voisinage ouvert contenant une infinité de points de l’intervalle, ce qui confirme qu’il est un point d’accumulation.
exemple de 0,5 comme point d’accumulation dans l’intervalle fermé [0,1]

Il en va de même pour les extrémités de l’intervalle. Par exemple, le point $0$ est un point d’accumulation de $[0,1]$, car tout voisinage de ce point renferme d’autres points de l’intervalle, comme $0,1$, $0,01$, $0,001$, etc.

Ainsi, tous les points de $[0,1]$ sont des points d’accumulation de cet ensemble.

Un ensemble $ A $ est fermé si et seulement si $ A = \overline{A} $
Dans un espace topologique, un ensemble $ A $ est fermé s’il est égal à sa clôture, c’est-à-dire $ A = \overline{A} $. La clôture de $ A $, notée $ \overline{A} $, comprend tous les points de $ A $ ainsi que ses points d’accumulation. Par définition, si un ensemble $ A $ contient tous ses points d’accumulation, alors il est fermé.

Et ainsi de suite.