Topologie Produit d'Espaces Topologiques

Étant donnés deux espaces topologiques $X$ et $Y$, la topologie produit sur $X \times Y$ est définie comme la topologie engendrée par la base $B$, formée des produits cartésiens d’ouverts de la forme $U \times V$, où $U$ est un ouvert de $X$ et $V$ un ouvert de $Y$. $$ B = \{ U \times V \mid U \text{ est ouvert dans } X \text{ et } V \text{ est ouvert dans } Y \} $$

Pour construire une topologie sur $X \times Y$, on commence par considérer les ensembles de la forme $U \times V$, avec $U$ ouvert dans $X$ et $V$ ouvert dans $Y$.

Cette famille d’ensembles, notée $B$, constitue une base d’une topologie.

On appelle base topologique toute collection d’ouverts telle que tout autre ouvert de l’espace $X \times Y$ puisse s’exprimer comme union d’éléments de cette collection.

Dans la topologie produit, le produit cartésien de deux ouverts est lui-même un ouvert.

Remarque : Les ouverts de la topologie produit ne se limitent pas aux produits cartésiens $U \times V$ d’ouverts de $X$ et de $Y$; ils comprennent également toutes les unions possibles de tels produits. Par conséquent, l’ensemble $B$ ne constitue pas une topologie en soi, mais seulement une base. Si l’on considérait $B$ comme une topologie complète, on omettrait une partie des ouverts générés par ces unions.

Ce principe s’applique également aux ensembles fermés.

Dans la topologie produit, le produit cartésien de deux ensembles fermés est aussi un ensemble fermé.

Cependant, tout fermé de la topologie produit ne peut pas nécessairement être exprimé sous forme d’un produit de fermés.

Autrement dit, comme pour les ouverts, certains fermés dans la topologie produit ne proviennent pas d’un produit cartésien d’ensembles fermés.

Un Exemple Concret
Produit de Plusieurs Espaces Topologiques
Base de la Topologie Produit
Remarques Finales

Un Exemple Concret

Examinons un exemple pour mieux saisir comment se construit la topologie produit.

Considérons les espaces topologiques suivants :

$X$ est la droite réelle $\mathbb{R}$ munie de sa topologie usuelle (dont les ouverts sont les intervalles ouverts $(a, b)$).
$Y$ est également $\mathbb{R}$, avec la même topologie usuelle.

Le produit $X \times Y$ correspond alors au plan cartésien $\mathbb{R}^2$.

Pour former la base $B$ de la topologie produit sur $X \times Y$, on considère tous les produits $U \times V$, où $U$ est un ouvert de $X$ et $V$ un ouvert de $Y$.

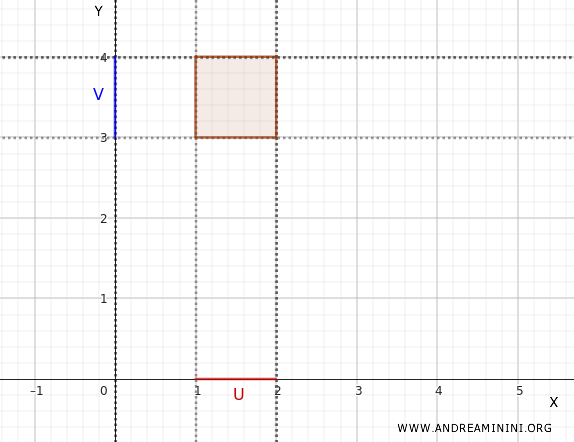
Par exemple, prenons $U = (1, 2) \subset X$, un intervalle ouvert de $X$.

Et soit $V = (3, 4) \subset Y$, également un intervalle ouvert de $Y$.

Alors, $U \times V = (1, 2) \times (3, 4)$ est un ouvert de $\mathbb{R}^2$. Cet ensemble représente un rectangle ouvert dans le plan cartésien.

rectangle ouvert dans le plan cartésien

Observons maintenant ce qui se passe si l’on prend l’union de deux ensembles de base.

Considérons $U_1 \times V_1 = (1, 2) \times (3, 4)$.

Puis $U_2 \times V_2 = (1.5, 2.5) \times (3.5, 4.5)$.

Ces deux ensembles représentent des rectangles ouverts dans le plan.

union de rectangles ouverts dans le plan

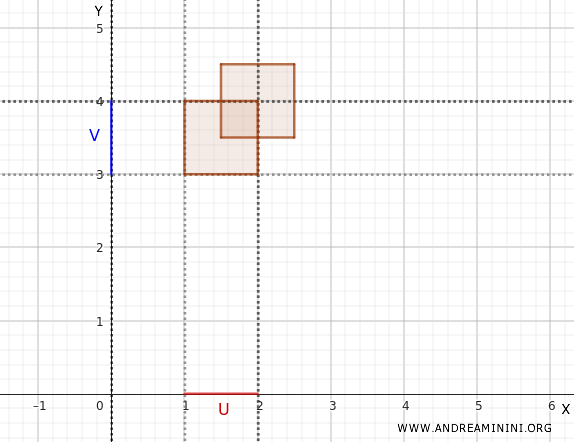
L’union de ces deux ensembles ne correspond plus à un simple produit cartésien $U \times V$, mais comme elle est formée par des éléments de la base, elle constitue malgré tout un ouvert de la topologie produit :

$$ (1, 2) \times (3, 4) \cup (1.5, 2.5) \times (3.5, 4.5) $$

Ainsi, tout point du plan peut être inclus dans une union d’ensembles de base de type $U \times V$.

Par exemple, considérons le point $(1.8, 3.8)$.

Ce point appartient à $ (1, 2) \times (3, 4) $, donc aussi à l’union des deux rectangles.

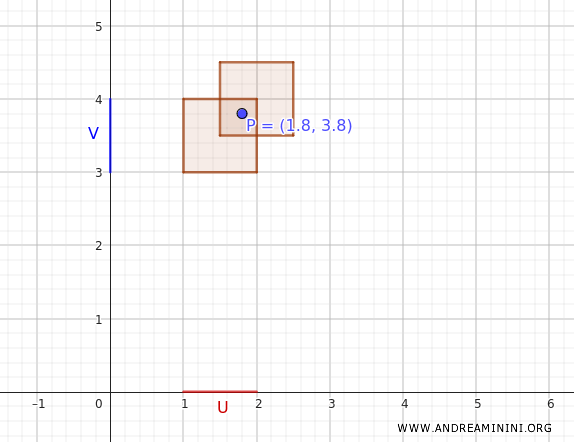
point inclus dans l’union d’ouverts de base

Cet exemple illustre clairement que la base $B$ engendre bien une topologie sur le produit $X \times Y$.

Remarque : Cette topologie, dite topologie produit, est précieuse car elle permet de conserver la structure ouverte des espaces $X$ et $Y$ lors de la construction du produit $X \times Y$.

Exemple 2

Considérons maintenant deux espaces topologiques finis :

$X = \{a, b, c\}$, muni de la topologie $\{\emptyset, \{a\}, \{b, c\}, X\}$
$Y = \{1, 2\}$, muni de la topologie $\{\emptyset, \{1\}, Y\}$

Pour déterminer la topologie produit sur $X \times Y$, on calcule tous les produits cartésiens entre ouverts de $X$ et de $Y$, puis on en prend toutes les unions possibles.

$$ B = \{ U \times V \mid U \text{ est ouvert dans } X \text{ et } V \text{ est ouvert dans } Y \} $$

Les ouverts de $X$ sont :

$\emptyset$
$\{a\}$
$\{b, c\}$
$X = \{a, b, c\}$

Les ouverts de $Y$ sont :

$\emptyset$
$\{1\}$
$Y = \{1, 2\}$

Calculons maintenant les produits cartésiens :

$\emptyset \times \emptyset = \emptyset$
$\emptyset \times \{1\} = \emptyset$
$\emptyset \times Y = \emptyset$
$\{a\} \times \emptyset = \emptyset$
$\{a\} \times \{1\} = \{(a, 1)\}$
$\{a\} \times Y = \{(a, 1), (a, 2)\}$
$\{b, c\} \times \emptyset = \emptyset$
$\{b, c\} \times \{1\} = \{(b, 1), (c, 1)\}$
$\{b, c\} \times Y = \{(b, 1), (b, 2), (c, 1), (c, 2)\}$
$X \times \emptyset = \emptyset$
$X \times \{1\} = \{(a, 1), (b, 1), (c, 1)\}$
$X \times Y = \{(a, 1), (a, 2), (b, 1), (b, 2), (c, 1), (c, 2)\}$

Remarque : Le produit cartésien de deux ensembles est l’ensemble des couples $(a, b)$ tels que $a \in A$ et $b \in B$. Formellement : \[ A \times B = \{(a, b) \mid a \in A \text{ et } b \in B\} \] Si l’un des deux ensembles est vide ($\emptyset$), aucun couple ne peut être formé, et le produit est vide : \[ \emptyset \times B = \{(a, b) \mid a \in \emptyset \text{ et } b \in B\} = \emptyset \]

La topologie produit est constituée de toutes les unions possibles de ces produits cartésiens. Par conséquent, dans $X \times Y$, elle inclut :

$\emptyset$
$\{(a, 1)\}$
$\{(a, 1), (a, 2)\}$
$\{(b, 1), (c, 1)\}$
$\{(b, 1), (b, 2), (c, 1), (c, 2)\}$
$\{(a, 1), (b, 1), (c, 1)\}$
$X \times Y = \{(a, 1), (a, 2), (b, 1), (b, 2), (c, 1), (c, 2)\}$
Toute autre union de ces ensembles
Par exemple : $\{(a, 1)\} \cup \{(b, 1), (c, 1)\} = \{(a, 1), (b, 1), (c, 1)\}$, etc.

La topologie produit sur $X \times Y$ est donc formée de toutes ces unions.

On constate ainsi que, dans la topologie produit, les ouverts ne se limitent pas aux simples produits $U \times V$; les unions de tels produits sont elles aussi des ouverts.

Par exemple : $\{(a, 1)\} \cup \{(b, 1), (c, 1)\} = \{(a, 1), (b, 1), (c, 1)\}$ est un ouvert dans la topologie produit. Il est donc incorrect de penser que seuls les produits $U \times V$ constituent les ouverts.

La base $B$ de la topologie sur $X \times Y$ est composée uniquement des produits cartésiens non vides.

$\{(a, 1)\}$
$\{(a, 1), (a, 2)\}$
$\{(b, 1), (c, 1)\}$
$\{(b, 1), (b, 2), (c, 1), (c, 2)\}$
$\{(a, 1), (b, 1), (c, 1)\}$
$X \times Y = \{(a, 1), (a, 2), (b, 1), (b, 2), (c, 1), (c, 2)\}$

Produit de Plusieurs Espaces Topologiques

Le concept de topologie produit s’étend naturellement au cas des produits de plusieurs espaces topologiques.

Étant donnés $ n $ espaces topologiques $ X_1, X_2, \dots, X_n $, si pour chaque $ i $, on considère une famille d’ouverts $ U_i \subseteq X_i $, alors l’ensemble de tous les produits cartésiens $ U_1 \times U_2 \times \cdots \times U_n $ constitue une base pour une topologie sur l’espace produit $ X_1 \times \cdots \times X_n $. $$ B = \{ U_1 \times U_2 \times \cdots \times U_n \mid U_i \text{ est ouvert dans } X_i \text{ pour tout } i \} $$

Base de la Topologie Produit

En général, le produit cartésien d’ouverts provenant de deux espaces topologiques forme une base valide pour la topologie produit.

$$ B = \{ U \times V \mid U \text{ est ouvert dans } X, \ V \text{ est ouvert dans } Y \} $$

Cependant, cette base peut s’avérer très étendue.

On dispose d’une méthode alternative, à la fois plus compacte et plus efficace, pour construire une base de la topologie produit.

Si $ B_X $ est une base de la topologie de $ X $ et $ B_Y $ une base de celle de $ Y $, alors l’ensemble des produits $ U \times V $, où $ U \in B_X $ et $ V \in B_Y $, forme une base de la topologie produit sur $ X \times Y $ : $$ B = \{ U \times V \mid U \in B_X, \ V \in B_Y \} $$

Ce système de base $ B $ engendre toute la topologie produit sur $ X \times Y $.

Autrement dit, les éléments de $ B $ sont les ouverts élémentaires de la topologie produit, et tout ouvert de cette topologie peut s’écrire comme union d’un certain nombre de ces produits cartésiens.

Remarque : Cette construction se généralise naturellement au cas de produits finis. Étant donnés $ n $ espaces topologiques $ X_1, X_2, \dots, X_n $, si $ B_i $ est une base pour la topologie de $ X_i $, alors l’ensemble des produits $ B_1 \times B_2 \times \cdots \times B_n $ constitue une base pour la topologie produit sur $ X_1 \times \cdots \times X_n $ : $$ B = \{ B_1 \times \cdots \times B_n \mid B_i \text{ est une base de } X_i, \ i = 1, \dots, n \} $$

Exemple

Considérons deux espaces topologiques finis :

L’espace $ X = \{a, b\} $, muni de la topologie $ \mathcal{T}_X = \{\emptyset, \{a\}, \{b\}, \{a, b\}\} $, dont la base minimale est $ B_X = \{\{a\}, \{b\}\} $.
L’espace $ Y = \{1, 2\} $, muni de la topologie $ \mathcal{T}_Y = \{\emptyset, \{1\}, \{2\}, \{1, 2\}\} $, dont la base minimale est $ B_Y = \{\{1\}, \{2\}\} $.

Pour former une base minimale de la topologie produit, il suffit de considérer les produits cartésiens des éléments de $ B_X $ et $ B_Y $, sans passer par tous les ouverts de $ X $ et $ Y $.

$$ B_X = \{\{a\}, \{b\}\}, \quad B_Y = \{\{1\}, \{2\}\} $$

Les produits cartésiens correspondants sont :

$$ \{a\} \times \{1\} = \{(a, 1)\}, \quad \{a\} \times \{2\} = \{(a, 2)\} $$

$$ \{b\} \times \{1\} = \{(b, 1)\}, \quad \{b\} \times \{2\} = \{(b, 2)\} $$

La base minimale de la topologie produit sur $ X \times Y $ est donc :

$$ B_{\text{min}} = \{\{(a, 1)\}, \{(a, 2)\}, \{(b, 1)\}, \{(b, 2)\}\} $$

Cette collection d’ensembles suffit à générer toute la topologie produit sur $ X \times Y $.

En résumé, en travaillant avec des ensembles atomiques - ceux qui ne peuvent être décomposés en ouverts strictement plus petits - on obtient une base concise qui décrit néanmoins entièrement la topologie produit.

Démonstration

Nous voulons montrer que l’ensemble $ B = \{U \times V \mid U \in B_X, V \in B_Y\} $ constitue bien une base pour la topologie produit sur $ X \times Y $.

On sait que $ B_X $ et $ B_Y $ sont des bases pour les topologies respectives de $ X $ et $ Y $.

Par définition, dans la topologie produit, les ouverts sont des unions d’ensembles de la forme $ U \times V $, où $ U \subseteq X $ et $ V \subseteq Y $ sont ouverts.

Pour établir que $ B $ est une base, il suffit de démontrer que tout ouvert $ W \subseteq X \times Y $ peut s’exprimer comme union d’éléments de $ B $.

Vérification de la propriété de base

Soit $ W $ un ouvert de la topologie produit, et soit $ (x, y) \in W $.

Alors, par définition, il existe un rectangle $ U' \times V' \subseteq W $, avec $ U' \subseteq X $ et $ V' \subseteq Y $ ouverts, tel que :

$$ (x, y) \in U' \times V' \subseteq W $$

Comme $ B_X $ est une base de $ X $, il existe $ U \in B_X $ tel que $ x \in U \subseteq U' $. De même, il existe $ V \in B_Y $ tel que $ y \in V \subseteq V' $.

On a donc :

$$ (x, y) \in U \times V \subseteq U' \times V' \subseteq W $$

Autrement dit, pour tout point de $ W $, il existe un élément de $ B $ qui le contient et qui est inclus dans $ W $.

Conclusion

Comme tout point de $ W $ est contenu dans un ensemble de la base $ B $ inclus dans $ W $, il s’ensuit que $ B $ engendre bien la topologie produit.

Par conséquent, l’ensemble $ B = \{U \times V \mid U \in B_X, V \in B_Y\} $ satisfait les conditions pour être une base de la topologie produit sur $ X \times Y $.

La démonstration est ainsi achevée.

Remarques Finales

Quelques résultats supplémentaires utiles dans le cadre de la topologie produit :

Théorème du Sous-espace Produit
Si $ A \subseteq X $ et $ B \subseteq Y $ sont des sous-espaces topologiques, alors la topologie induite sur $ A \times B $, considéré comme sous-ensemble de $ X \times Y $, coïncide avec la topologie produit construite à partir des topologies sous-espaces de $ A $ et $ B $. $$ \quad \tau_{A \times B}^{\text{sub}} = \tau_A^{\text{sub}} \times \tau_B^{\text{sub}} $$
Équivalence Topologique des Produits
Pour trois espaces $ X, Y, Z $, les espaces $ (X \times Y) \times Z $, $ X \times (Y \times Z) $ et $ X \times Y \times Z $ sont homéomorphes. Autrement dit, l’ordre des parenthésages n’affecte pas la structure topologique du produit. $$ (X \times Y) \times Z \cong X \times (Y \times Z) \cong X \times Y \times Z $$
Théorème de l’Intérieur d’un Produit Cartésien
Pour deux ensembles $ A \subseteq X $ et $ B \subseteq Y $, l’intérieur de leur produit cartésien est égal au produit de leurs intérieurs respectifs : $$ \text{Int}(A \times B) = \text{Int}(A) \times \text{Int}(B) $$