Théorème sur l’Intérieur d’un Produit Cartésien
Soient \(A\) et \(B\) deux ensembles inclus respectivement dans les espaces topologiques \(X\) et \(Y\). L’intérieur de leur produit cartésien \(A \times B\) est égal au produit de leurs intérieurs respectifs. Autrement dit : $$ \text{Int}(A \times B) = \text{Int}(A) \times \text{Int}(B) $$
Cette propriété s’applique en particulier lorsque \(A\) et \(B\) sont des ouverts, dans le cadre du produit de deux espaces topologiques.
En des termes plus intuitifs, le théorème affirme que, pour deux ensembles \(A\) et \(B\) appartenant à des espaces topologiques \(X\) et \(Y\), l’intérieur de leur produit cartésien s’obtient en prenant simplement le produit de leurs intérieurs.
Un Exemple Concret
Considérons les espaces topologiques \(X = \mathbb{R}\) et \(Y = \mathbb{R}\), ainsi que les sous-ensembles \(A = (0, 2)\) et \(B = (1, 3)\).
On observe que \(A\) et \(B\) sont des intervalles ouverts de la droite réelle \(\mathbb{R}\).
Commençons par déterminer l’intérieur de chacun de ces ensembles.
L’intérieur de \(A\) est \((0, 2)\), puisque l’ensemble est déjà un ouvert :
$$ \text{Int}(A) = (0, 2) $$
De même, l’intérieur de \(B\) est \((1, 3)\) :
$$ \text{Int}(B) = (1, 3) $$
Calculons maintenant le produit des intérieurs :
$$ \text{Int}(A) \times \text{Int}(B) = (0, 2) \times (1, 3) $$
Cet ensemble correspond à l’ensemble des couples \((x, y)\) tels que \(x \in (0, 2)\) et \(y \in (1, 3)\) :
$$ \text{Int}(A) \times \text{Int}(B) = \{(x, y) \mid x \in (0, 2),\ y \in (1, 3)\} $$
Il s’agit d’un rectangle ouvert dans le plan \(\mathbb{R}^2\), délimité par les points \((0, 1)\), \((0, 3)\), \((2, 1)\) et \((2, 3)\).
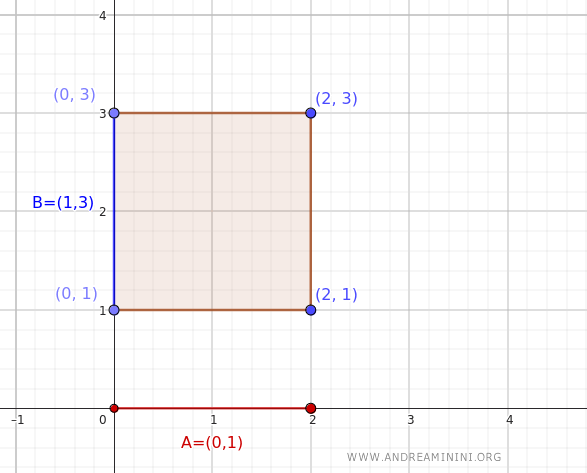
Déterminons maintenant l’intérieur du produit cartésien \(A \times B = (0, 2) \times (1, 3)\) :
On retrouve exactement le même ensemble : un rectangle ouvert dans \(\mathbb{R}^2\).
On en conclut que l’intérieur du produit \(A \times B\) est bien égal au produit des intérieurs de \(A\) et \(B\) :
$$ \text{Int}(A \times B) = (0, 2) \times (1, 3) = \text{Int}(A) \times \text{Int}(B) $$
Cet exemple illustre clairement la validité du théorème.
Démonstration
La démonstration repose sur une double inclusion. Nous allons d’abord montrer que l’intérieur du produit contient le produit des intérieurs, puis qu’il y est également contenu, ce qui permettra de conclure à l’égalité.
1] Le produit des intérieurs est contenu dans l’intérieur du produit
Nous souhaitons montrer que :
$$ \text{Int}(A) \times \text{Int}(B) \subseteq \text{Int}(A \times B) $$
Autrement dit, pour tout couple \((x, y)\) avec \(x \in \text{Int}(A)\) et \(y \in \text{Int}(B)\), il faut que \((x, y) \in \text{Int}(A \times B)\).
Puisque \(x\) est un point intérieur de \(A\), il existe un ouvert \(U \subseteq X\) tel que \(x \in U \subseteq A\).
De même, comme \(y \in \text{Int}(B)\), il existe un ouvert \(V \subseteq Y\) tel que \(y \in V \subseteq B\).
Le produit \(U \times V\) est alors un ouvert de \(X \times Y\) contenant \((x, y)\), et \(U \times V \subseteq A \times B\).
On en déduit que \((x, y)\) est un point intérieur de \(A \times B\), ce qui prouve l’inclusion :
$$ \text{Int}(A) \times \text{Int}(B) \subseteq \text{Int}(A \times B) $$
2] L’intérieur du produit est contenu dans le produit des intérieurs
Nous allons maintenant établir que :
$$ \text{Int}(A \times B) \subseteq \text{Int}(A) \times \text{Int}(B) $$
Ce qui revient à démontrer que, si \((x, y) \in \text{Int}(A \times B)\), alors \(x \in \text{Int}(A)\) et \(y \in \text{Int}(B)\).
Soit \((x, y) \in \text{Int}(A \times B)\). Par définition, il existe un ouvert \(W \subseteq X \times Y\) tel que \((x, y) \in W \subseteq A \times B\).
Or, la topologie produit admet une base constituée des produits \(U \times V\), avec \(U \subseteq X\) ouvert et \(V \subseteq Y\) ouvert, tels que \((x, y) \in U \times V \subseteq W\).
De l’inclusion \(U \times V \subseteq A \times B\) on déduit \(U \subseteq A\) et \(V \subseteq B\), donc \(x \in \text{Int}(A)\) et \(y \in \text{Int}(B)\).
On en conclut que \((x, y) \in \text{Int}(A) \times \text{Int}(B)\), ce qui démontre :
$$ \text{Int}(A \times B) \subseteq \text{Int}(A) \times \text{Int}(B) $$
3] Conclusion
Les deux inclusions étant établies :
$$ \text{Int}(A) \times \text{Int}(B) \subseteq \text{Int}(A \times B) $$
$$ \text{Int}(A \times B) \subseteq \text{Int}(A) \times \text{Int}(B) $$
On en déduit que :
$$ \text{Int}(A \times B) = \text{Int}(A) \times \text{Int}(B) $$
Ce qui achève la démonstration du théorème.