Points fixes en topologie
En topologie, on parle de point fixe pour désigner une valeur qui reste invariante sous l'action d'une fonction.
Autrement dit, si l'on considère une fonction f(x), un point p est fixe si f(p) = p, ce qui signifie que le résultat de la fonction est identique à son entrée lorsque p est appliqué.
$$ f(p) = p $$
Imaginez la rotation d'un objet autour d'un point central P.
Cette rotation assigne de nouvelles coordonnées aux points de l'objet dans l'espace.
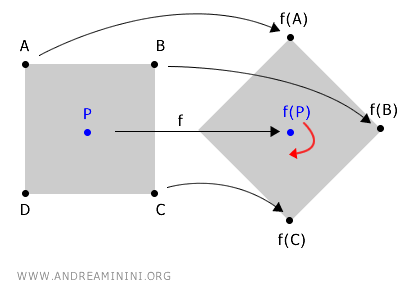
Dans ce cas, le centre de rotation, P, est un point fixe puisque ses coordonnées ne changent pas sous l'effet de la fonction de rotation f(P).
$$ f(P) \longrightarrow P $$
Les points fixes occupent une place essentielle dans divers champs mathématiques et leurs applications, incluant l'analyse numérique, la théorie des jeux et l'économie.
Un exemple illustre en topologie est le théorème du point fixe de Brouwer.
Illustration pratique
Considérons la fonction f(x) = sin(x) sur l'intervalle fermé [0, 2π] radians.
$$ f(x) = \sin(x) $$
Le point fixe de cette fonction à p=0 radians est immédiat puisque sin(0) = 0.
$$ \sin(0) = 0 $$
La sortie est donc directement le reflet de l'entrée.
Exemple 2
Considérons maintenant la fonction f(x) = cos(x) sur le même intervalle [0, 2π] radians.
$$ f(x) = \cos(x) $$
Ici, x=0 n'est pas un point fixe car cos(0) = 1, ce qui révèle une non-concordance entre l'entrée et la sortie.
Le point fixe pour la fonction f(x) = cos(x) se trouve approximativement à x = 0.73908513 radians.
$$ \cos(0.73908513) = 0.73908513 $$
Ainsi, cos(0.73908513) est pratiquement égal à 0.73908513.
Le théorème du point fixe de Brouwer
Ce théorème énonce :
Toute fonction continue qui projette un intervalle fermé en n dimensions assure l'existence d'au moins un point fixe.
Il s'agit d'un théorème d'existence qui met en évidence la certitude d'avoir au moins un point fixe, sans pour autant localiser précisément où il se trouve.
Ce concept a de larges implications, notamment dans la démonstration de l'existence de points d'équilibre dans les systèmes dynamiques et les modèles économiques.
Et ainsi de suite.