La Base d'une Topologie

Une base d'une topologie est une collection \( B \) d’ensembles ouverts telle que tout ouvert de l’espace topologique \( T \) puisse s’écrire comme une réunion d’éléments de \( B \).

Soit un ensemble \( X \), muni d’une collection \( T \) de sous-ensembles définissant une topologie sur \( X \). Dans ce cadre, une base de la topologie \( T \) est une collection \( B \) d’ensembles, appelés ensembles de base, vérifiant les deux conditions suivantes :

• Tout élément \( x \in X \) appartient à au moins un ensemble de \( B \).
• Si \( x \in B_1 \cap B_2 \), où \( B_1, B_2 \in B \) et \( B_1 \cap B_2 \ne \varnothing \), alors il existe \( B_3 \in B \) tel que \( x \in B_3 \subseteq B_1 \cap B_2 \). Autrement dit, l’intersection doit contenir un ensemble de base incluant \( x \).
  

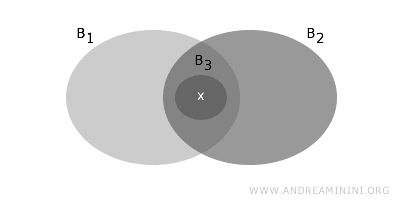
Ces deux propriétés garantissent que la collection \( B \) définit bien une base pour la topologie \( T \).

Pourquoi est-ce important ?

La notion de base est fondamentale car elle permet de décrire la topologie \( T \) à partir d’un ensemble plus restreint d’ensembles « générateurs », sans avoir à énumérer directement tous les ouverts.

Remarque : La condition sur les intersections garantit que la topologie vérifie les axiomes essentiels, notamment que l’intersection de deux ouverts est encore un ouvert.

Un exemple concret

Considérons l’ensemble suivant :

$$ X = \{a, b, c \} $$

et la topologie :

$$ T = \{ \emptyset, \{ a \}, \{ b,c \}, \{ a,b,c \} \} $$

Cette collection \( T \) correspond à l’ensemble des ouverts définis sur \( X \).

Une base \( B \) possible pour cette topologie est :

$$ B = \{ \{ a \}, \{ b,c \} \} $$

Ce choix est valide car chaque élément de \( X \) appartient à au moins un ensemble de \( B \), et tout ouvert de \( T \) peut s’exprimer comme une réunion d’éléments de \( B \).

Exemples :

• \( \{a\} \in B \)
• \( \{b,c\} \in B \)
• \( \{a,b,c\} = \{a\} \cup \{b,c\} \)

Remarque : En théorie des ensembles, l’ensemble vide (Ø) est un sous-ensemble impropre de tout ensemble, et appartient donc toujours à la topologie. Par définition, l’ensemble vide est considéré comme ouvert dans toute topologie : $$ \emptyset \in T $$

Cet exemple illustre bien le concept de base dans un cadre fini. Dans des contextes plus généraux, notamment pour des ensembles infinis, la construction d’une base peut se révéler plus délicate. Mais le principe fondamental reste identique : une base fournit les « briques élémentaires » à partir desquelles on génère l’ensemble des ouverts.

Autre approche

Une autre base possible pour la topologie définie sur \( X = \{a, b, c\} \) est :

$$ B = \{ \{ a \}, \{ b \}, \{ c \} \} $$

Il s’agit ici des singletons de \( X \).

Vérifions que \( B \) forme bien une base pour la topologie \( T = \{ \varnothing, X, \{a\}, \{b,c\} \} \) :

• \( \varnothing \) est ouvert par définition et présent dans toute topologie.
• \( \{a\} \in B \)
• \( \{b,c\} = \{b\} \cup \{c\} \)
• \( X = \{a,b,c\} = \{a\} \cup \{b\} \cup \{c\} \)

Par conséquent, \( B \) est bien une base de la topologie définie sur \( X \), puisque tout ouvert peut s’y reconstruire par unions d’éléments de \( B \).

Remarque : Ce cas illustre que plusieurs bases peuvent exister pour une même topologie. Chacune permet une description différente de la structure des ouverts à partir d’éléments fondamentaux.

Exemple 2

Considérons à présent la base usuelle de la topologie usuelle sur la droite réelle, constituée de tous les intervalles ouverts :

$$ B = \{ (a,b) \subseteq \mathbb{R} \mid a < b \} $$

Cette collection forme une base car tout point de \( \mathbb{R} \) appartient à un certain intervalle ouvert \( (a,b) \).

De plus, l’intersection de deux intervalles ouverts contenant un même point contient toujours un sous-intervalle ouvert autour de ce point, ce qui satisfait à la deuxième condition de base.

Par exemple, considérons \( (0,3) \) et \( (2,4) \). Leur intersection est \( (2,3) \), un intervalle ouvert appartenant à \( B \) :

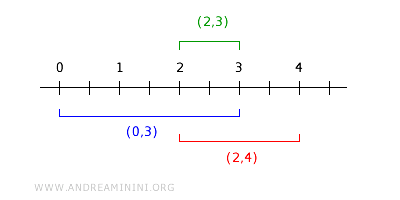
On a bien : $$ (0,3) \cap (2,4) = (2,3) \in B $$ ce qui montre que \( B \) est stable par intersection locale.

Remarques

Quelques considérations supplémentaires à propos des bases topologiques :

• Si, pour un ensemble \( X \), on construit une base \( B \) contenant les singletons \( \{x\} \) pour chaque \( x \in X \), alors on peut générer une topologie sur \( X \).

  En effet, les unions de singletons permettent de former toutes sortes de topologies.
  
  Par exemple, la base \( B = \{ \{a\}, \{b\}, \{c\} \} \) sur \( X = \{a,b,c\} \) permet de générer la topologie \( T = \{ \varnothing, \{a\}, \{b,c\}, X \} \).
  
  Mais cette même base peut également engendrer d’autres topologies sur \( X \), telles que :
  • La topologie \( T = \{ \varnothing, \{b\}, \{a,c\}, X \} \)
  • La topologie triviale \( T = \{ \varnothing, X \} \)
  • La topologie discrète \( T = \{ \varnothing, \{a\}, \{b\}, \{c\}, \{a,b\}, \{a,c\}, \{b,c\}, X \} \)

  Remarque : La première condition est bien remplie, car chaque élément de \( X \) est inclus dans un singleton de \( B \). La seconde l’est également, puisque les singletons sont disjoints et ne contiennent chacun qu’un seul élément.

Ce principe se généralise à tout ensemble, fini ou infini, et à toute topologie construite à partir d’une base.