Boule ouverte
En topologie, une boule ouverte - également appelée voisinage circulaire, disque ou sphère ouverte - est l’ensemble des points situés à une distance strictement inférieure à un certain rayon \( r \) d’un point donné, appelé centre \( c \) : $$ B(c, r) = \{ x \in M \mid d(c, x) < r \} $$
Ce concept s’inscrit dans le cadre d’un espace métrique \( M \), où \( d \) désigne une métrique, c’est-à-dire une fonction qui mesure la distance entre deux points de l’espace.
Une boule ouverte est entièrement déterminée par son centre et son rayon.
Elle est dite « ouverte » au sens topologique, car tout point qu’elle contient admet lui-même une boule strictement incluse dans la boule initiale.
Remarque : Les boules ouvertes sont invariantes par translation et homothétie : les déplacer ou modifier leur échelle ne change pas leur nature topologique.
Considérons le plan \( \mathbb{R}^2 \). La distance entre un point \( p = (x, y) \) et un centre \( c = (x_0, y_0) \) est donnée par la métrique euclidienne :
$$ d(p,c) = \sqrt{(x - x_0)^2 + (y - y_0)^2} $$
Les boules ouvertes jouent un rôle central dans la définition de la structure topologique des espaces métriques. En particulier, elles forment une base de la topologie usuelle du plan \( \mathbb{R}^2 \).
Cette topologie est engendrée par la famille suivante :
$$ B = \{ B(p, r) \ | \ p \in \mathbb{R}^2,\ r > 0 \} $$
Ici, \( p \) est un point du plan et \( r \) désigne le rayon de la boule.

Parmi les nombreuses topologies possibles sur \( \mathbb{R}^2 \), celle induite par les boules ouvertes euclidiennes est de loin la plus couramment utilisée.
Dans toute boule ouverte \( B(p,r) \), chaque point \( q \in B(p,r) \) est le centre d’une boule plus petite \( B(q, \epsilon) \) entièrement contenue dans \( B(p,r) \).
Ce fait se formalise ainsi :
$$ \forall\ q \in B(p,r),\ \exists\ \epsilon > 0\ \text{tel que}\ B(q,\epsilon) \subset B(p,r) $$
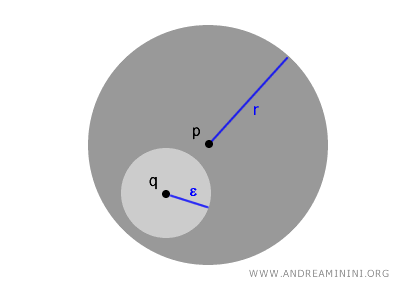
Ce processus peut être itéré indéfiniment, illustrant la nature locale des boules ouvertes dans la structure d’un espace topologique.