Points d’accumulation en topologie

Dans un espace topologique $X$, un point $x$ est appelé point d’accumulation d’un sous-ensemble $A \subseteq X$ si tout voisinage de $x$ rencontre $A$ en au moins un point distinct de $x$.

Autrement dit, dans tout voisinage de $x$, il existe toujours au moins un point de $A$ différent de $x$.

Plus formellement, $x$ est un point d’accumulation si l’intersection de tout voisinage $U$ de $x$ avec $A$ est non vide.

$$ U \cap A \neq \emptyset $$

Un point d’accumulation ne fait pas nécessairement partie de $A$ ; il peut être extérieur à l’ensemble.

Dans le cadre de l’espace topologique réel $\mathbb{R}$, la notion de point d’accumulation est particulièrement intuitive. Sur la droite réelle, un point $x$ est un point d’accumulation d’un sous-ensemble $A$ si tout voisinage de $x$, c’est-à-dire tout intervalle ouvert du type $(x-\epsilon, x+\epsilon)$, contient au moins un point de $A$ distinct de $x$.
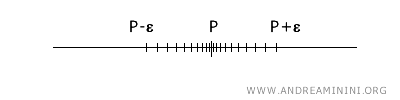
ilustración de un punto de acumulación sobre la recta real
La définition topologique du point d’accumulation généralise ce concept à l’espace $n$-dimensionnel $\mathbb{R}^n$. Dans ce contexte, un point $x$ est un point d’accumulation d’un ensemble $A$ si tout voisinage de $x$ possède une intersection non vide avec $A$ en un point autre que $x$ lui-même. Cette généralisation peut toutefois paraître moins intuitive en dimensions supérieures.

Exemples concrets
Remarques

Exemples concrets

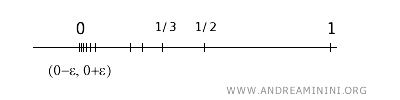
Considérons l’ensemble $A$ comme sous-ensemble de $\mathbb{R}$ muni de la topologie usuelle.

$$ A = \left\{ \frac{1}{n} \mid n \in \mathbb{N}^+ \right\} $$

Ce sous-ensemble comprend les points $ \frac{1}{1}, \frac{1}{2}, \frac{1}{3}, \ldots $, autrement dit $\{1, \frac{1}{2}, \frac{1}{3}, \frac{1}{4}, \ldots \}$.

Pour savoir si $0$ est un point d’accumulation de $A$, examinons un voisinage ouvert quelconque de $0$.

Tout voisinage de $0$ contient un intervalle ouvert $(a, b)$ tel que $a < 0 < b$.

Comme $\frac{1}{n}$ tend vers $0$ lorsque $n$ tend vers l’infini, il existe toujours un certain $\frac{1}{n}$ dans $(a, b)$ pour $n$ assez grand.

En conséquence, tout voisinage de $0$ contient au moins un point de $A$ distinct de $0$.

On en déduit que $0$ est un point d’accumulation de l’ensemble $A$.

representación de un punto de acumulación

Exemple 2

Considérons à présent l’ensemble $B$, également sous-ensemble de $\mathbb{R}$ muni de la topologie usuelle.

$$ B = \left\{ n + \frac{1}{n} \mid n \in \mathbb{N}^+ \right\} $$

Cet ensemble contient les points $ 1 + 1, 2 + \frac{1}{2}, 3 + \frac{1}{3}, \ldots $, c’est-à-dire $\{2, 2.5, 3.333\ldots, \ldots \}$.

Intéressons-nous au point $1$.

Tout voisinage ouvert de $1$ contient nécessairement un intervalle $(a, b)$ avec $a < 1 < b$.

Cependant, tous les éléments de $B$ sont strictement supérieurs à $1$. Pour qu’un élément de $B$ appartienne à $(a, b)$, il faudrait que $n + \frac{1}{n}$ soit compris entre $a$ et $b$.

Or, aucun élément de $B$ n’est inférieur ou égal à $1$, si bien qu’aucun voisinage de $1$ ne contient de points de $B$.

On conclut donc que $1$ n’est pas un point d’accumulation de $B$.

Exemple 3

Considérons l’ensemble $(0, 1]$ comme sous-ensemble de $\mathbb{R}$ muni de la topologie usuelle.

Nous souhaitons déterminer quels sont les points d’accumulation de $(0, 1]$.

D’après la définition, un point $x$ est un point d’accumulation de $(0, 1]$ si tout voisinage de $x$ rencontre $(0, 1]$ en au moins un point distinct de $x$.

Points intérieurs de $(0,1]$
Soit $x \in (0, 1]$. Tout voisinage de $x$ contient un intervalle ouvert $(a, b)$ tel que $a < x < b$. Comme $x$ appartient à $(0, 1]$, ce voisinage intersecte nécessairement $(0, 1)$ en des points distincts de $x$. Par conséquent, tout point $x \in (0, 1]$ est un point d’accumulation de $(0, 1]$.
Points frontières de $(0,1]$
Examinons maintenant les extrémités de l’intervalle : $0$ et $1$.
- Point $0$ : Bien que $0$ n’appartienne pas à $(0, 1]$, tout voisinage de $0$ contient un intervalle $(a, b)$ avec $a < 0 < b$, incluant donc une infinité de points strictement positifs appartenant à $(0, 1]$. Ainsi, $0$ est un point d’accumulation de $(0, 1]$.

- Point $1$ : Comme $1$ appartient à $(0, 1]$, tout voisinage de $1$ - par exemple un intervalle ouvert $(a, b)$ avec $a < 1 < b$ - contient une infinité de points de $(0, 1)$, différents de $1$. Par conséquent, $1$ est également un point d’accumulation de $(0, 1]$.
Points extérieurs à $[0, 1]$
Pour être complet, considérons tout point $x \notin [0, 1]$. Si $x < 0$ ou $x > 1$, il est toujours possible de trouver un voisinage de $x$ disjoint de $(0, 1]$.
Par exemple, si $x < 0$, on peut choisir un intervalle ouvert $(x - \epsilon, x + \epsilon)$ avec $\epsilon$ suffisamment petit pour qu’il ne contienne aucun point de $(0, 1]$. De même, si $x > 1$, il existe un intervalle ouvert centré sur $x$ entièrement disjoint de $(0, 1]$. Ainsi, aucun point extérieur à l’intervalle fermé $[0, 1]$ n’est un point d’accumulation de $(0, 1]$.

En conclusion, les points d’accumulation de $(0, 1]$ dans l’espace topologique $\mathbb{R}$, muni de la topologie usuelle, sont exactement les éléments de l’intervalle fermé $[0, 1]$.

Exemple 4

Déterminons maintenant l’ensemble des points d’accumulation de $ A = (0, 1] $ dans la topologie du bord inférieur sur $ \mathbb{R} $.

La topologie du bord inférieur sur $ \mathbb{R} $ est engendrée par les intervalles de la forme $[a, b)$ avec $ a < b $. Les ouverts de cette topologie sont donc des unions arbitraires de tels intervalles.

Un point $x$ est un point d’accumulation d’un ensemble $A$ si tout voisinage de $x$ contient au moins un point de $A$ distinct de $x$.

Examinons les différents cas :

Pour $x \in (0, 1)$
Tout voisinage de $x$ dans cette topologie est de la forme $[x, x + \epsilon)$, lequel contient une infinité de points de $A$. Ainsi, $x$ est bien un point d’accumulation de $A$.
Pour $x = 1$
Bien que la topologie du bord inférieur ne comporte pas d’intervalles de la forme $(1 - \epsilon, 1]$, il existe des voisinages de $1$ du type $[1 - \epsilon, 1)$, qui contiennent des points de $A$. Par conséquent, $1$ est également un point d’accumulation de $A$.
Pour $x = 0$
Tout voisinage de $0$, de la forme $[0, 0 + \epsilon)$, rencontre $A$ en une infinité de points. Ainsi, $0$ est aussi un point d’accumulation de $A$.
Pour $x < 0$ ou $x > 1$
Dans ces cas, aucun voisinage de la forme $[x, x + \epsilon)$ n’intersecte $A$. Ces points ne peuvent donc pas être des points d’accumulation.

En résumé, les points d’accumulation de l’ensemble $ A = (0, 1] $ dans la topologie du bord inférieur sur $ \mathbb{R} $ coïncident exactement avec les éléments de l’intervalle fermé $[0, 1]$.

Autrement dit, l’ensemble des points d’accumulation de $ A $ est $[0, 1]$.

Remarques

Voici quelques précisions importantes concernant les points d’accumulation :

L’adhérence d’un ensemble est l’union de l’ensemble et de ses points d’accumulation
L’adhérence d’un sous-ensemble $A$ d’un espace topologique $X$ est donnée par l’union de $A$ avec l’ensemble $A'$ de ses points d’accumulation : $$ \text{Cl}(A) = A \cup A' $$ En d’autres termes, $\text{Cl}(A)$ contient tous les points de $A$ ainsi que tous ceux qui sont limites de suites (ou plus généralement de filtres ou de réseaux) d’éléments de $A$.
Une suite peut converger vers un point d’accumulation
Si $ A $ est un sous-ensemble de $ X = \mathbb{R} $, muni de la topologie usuelle, et si $ x $ est un point d’accumulation de $ A $, alors il existe une suite $ \{x_i\} \subseteq A \setminus \{x\} $ qui converge vers $ x $. Il faut souligner que le point d’accumulation n’appartient pas nécessairement à l’ensemble $ A $ ; il peut très bien en être extérieur.
Unicité de la limite
Dans la topologie usuelle sur $ \mathbb{R} $, la limite d’une suite - lorsqu’elle existe - est unique. Cependant, cette propriété ne vaut pas dans toutes les topologies : dans des espaces non hausdorff, par exemple, une même suite peut converger vers plusieurs points différents. L’unicité de la limite dépend donc des propriétés de séparation de l’espace topologique étudié.

Ces observations permettent de mieux appréhender le rôle essentiel que jouent les points d’accumulation dans la structure topologique des ensembles.