Topologie Numérique
La topologie numérique (digital topology) s’intéresse aux structures topologiques définies sur des espaces discrets, tels qu’une grille de points (pixels en 2D ou voxels en 3D), en décrivant les relations de connexité entre eux selon une notion d’adjacence donnée.
Dans ce contexte, les ensembles ouverts se définissent par les connexions entre points, le type de connexité dépendant de critères tels que la connexité 4 ou 8 (en 2D) ou encore la connexité 6, 18 ou 26 (en 3D).
La topologie numérique trouve de larges applications dans des domaines comme le traitement d’images, les graphismes informatiques et la vision par ordinateur, puisqu’elle transpose les concepts de la topologie classique à des environnements discrets.
Ensembles Ouverts en Topologie Numérique
En topologie numérique, un ensemble \(U\) est dit ouvert si, pour chaque point \(x \in U\), tous ses points adjacents - selon la règle de connexité choisie - appartiennent également à \(U\).
La notion d’« adjacence » ou de « voisinage » entre points varie selon le type de connexité adopté dans l’espace numérique. Par exemple :
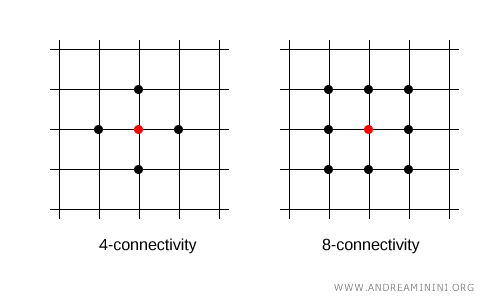
Sur une grille circulaire ou annulaire, chaque point est adjacent à deux autres, ce qui correspond à une structure de connexité 2.
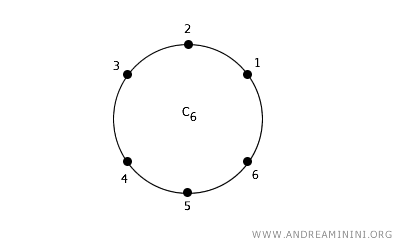
Dans un plan 2D, un point peut être relié à quatre voisins (connexité 4) - nord, sud, est et ouest - ou à huit voisins (connexité 8), en incluant les diagonales.
Dans un espace numérique tridimensionnel (3D), la connexité entre points peut suivre des critères de connexité 6, 18 ou 26, selon le nombre de voisins pris en compte.
Exemple
Considérons un ensemble de points disposés en cercle (dans un espace discret) avec une connexité de 2.
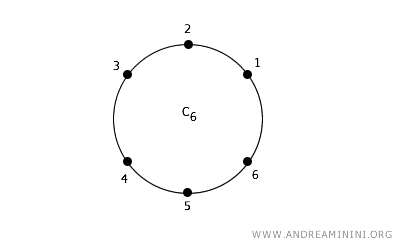
Dans ce cas, chaque point possède deux voisins immédiats, l’un à gauche et l’autre à droite.
Par exemple, le point 2 est adjacent aux points 1 et 3.

Un ensemble \(U\) est alors ouvert en topologie numérique si tous les voisins de chaque point de \(U\) appartiennent eux aussi à \(U\).
Ce concept transpose, dans un espace discret, l’idée de continuité et de liaison entre les points.
Différence entre Topologie Numérique et Topologie Discrète
Bien que la topologie numérique et la topologie discrète s’appliquent toutes deux à des espaces discrets, elles présentent des différences fondamentales :
- Topologie Discrète
Une topologie sur un ensemble \(X\) est dite discrète lorsque chaque sous-ensemble de \(X\) est ouvert. - Topologie Numérique
En revanche, en topologie numérique, un sous-ensemble n’est ouvert que s’il satisfait aux conditions de connexité imposées entre les points.
Quelle est, dès lors, la différence essentielle ?
Dans la topologie discrète, tout sous-ensemble est ouvert. En topologie numérique, seuls sont ouverts les ensembles qui respectent les critères de connexité définis.
En d’autres termes, la topologie numérique n’est pas équivalente à la topologie discrète, car tous les sous-ensembles ne sont pas automatiquement ouverts.
Par exemple, un ensemble formé de deux pixels isolés - sans lien entre eux - ne serait pas ouvert en topologie numérique, alors qu’il le serait dans une topologie discrète.
En résumé, la topologie numérique est conçue pour traduire la notion de connexité entre points dans un espace numérique, tandis que la topologie discrète considère chaque point comme une entité autonome, dépourvue de relations d’adjacence.
Exemple
Considérons l’ensemble de points \(\{1, 2, 3, 4\}\) disposés en cercle, avec une topologie numérique fondée sur une connexité de 2.
- L’ensemble \(\{1, 2\}\) est ouvert en topologie numérique, car les points 1 et 2 sont adjacents.
- L’ensemble \(\{1, 3\}\) ne l’est pas, car les points 1 et 3 ne sont pas directement reliés.
Si l’on étudie ces mêmes points \(\{1, 2, 3, 4\}\) dans le cadre d’une topologie discrète, aussi bien \(\{1, 2\}\) que \(\{1, 3\}\) seraient ouverts, puisque dans ce cas tout sous-ensemble est ouvert.
Remarque. Dans ce même espace métrique discret \(\{1, 2, 3, 4\}\), la topologie numérique est plus restrictive que la topologie discrète, car elle impose une condition de connexité pour qu’un ensemble soit ouvert.
Et ainsi de suite.