Sous-espace topologique

Un sous-espace topologique est une partie d’un espace topologique à laquelle on associe naturellement une topologie induite par celle de l’espace d’origine.

Soit $ (X, T) $ un espace topologique, où $ X $ est un ensemble et $ T $ une collection d’ouverts définissant la topologie sur $ X $. Si $ Y \subseteq X $, on définit la topologie induite sur $ Y $ par : \[ T_Y = \{ U \cap Y \mid U \in T \} \]

Autrement dit, un ensemble $ V \subseteq Y $ est ouvert dans la topologie induite si et seulement s’il peut s’écrire comme l’intersection d’un ouvert $ U $ de $ X $ avec $ Y $.

Ainsi, les ouverts de la topologie de sous-espace $ Y $ sont tous de la forme $ U \cap Y $, avec $ U $ ouvert dans $ X $.

$$ V_{open \ in \ Y} = U \cap Y $$

De manière analogue, les fermés dans la topologie induite sur $ Y $ sont les ensembles de la forme $ C \cap Y $, où $ C $ est fermé dans $ X $.

$$ V_{closed \ in \ Y} = C \cap Y $$

Remarque : Un ensemble peut être ouvert dans $ Y $ sans l’être dans $ X $. De même, certains ensembles peuvent être ouverts dans l’un mais fermés dans l’autre, ou bien simultanément ouverts et fermés dans les deux. Il existe aussi des ensembles dits « clopens » (ouverts et fermés à la fois). Un exemple de ce type est présenté plus loin pour illustrer ce phénomène.

Exemple concret
Propriétés de la topologie induite
Remarques

Exemple concret

Considérons $ \mathbb{R} $ muni de sa topologie usuelle, où les ouverts sont les intervalles ouverts.

Soit $ Y = [0, 1] $, un sous-ensemble de $ \mathbb{R} $.

La topologie induite sur $ Y $ contient les ensembles de la forme :

$$ U \cap [0, 1] $$

où $ U $ est un ouvert de $ \mathbb{R} $.

Par exemple, l’ensemble (-1, 0.5) est un ouvert dans $ \mathbb{R} $.

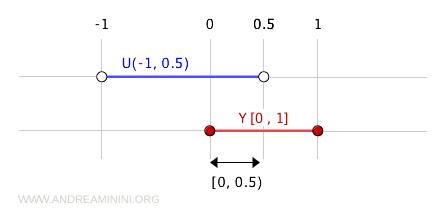
example

Son intersection avec $ Y = [0, 1] $ donne un ouvert de la topologie induite :

$$ (-1, 0.5) \cap [0, 1] = [0, 0.5) $$

Ainsi, l’ensemble $ [0, 0.5) $ est ouvert dans le sous-espace $ Y $.

À l’inverse, $ [0, 0.5] $ est fermé dans la topologie de sous-espace car il s’écrit comme l’intersection de $ [-1, 0.5] $, fermé dans $ \mathbb{R} $, avec $ Y $ :

$$ [-1, 0.5] \cap [0, 1] = [0, 0.5] $$

En résumé, la topologie induite sur $ Y $ hérite de celle de $ X $ de manière à ce que les ouverts soient des intersections avec des ouverts de $ X $.

Remarque : Les ensembles du type [0,a) ou (a,1], avec $ 0 < a < 1 $, ne sont pas ouverts dans $ \mathbb{R} $, mais ils le deviennent dans $ Y = [0,1] $, car ils peuvent s’obtenir comme intersections avec un ouvert de $ \mathbb{R} $. Par exemple, l’ouvert $ (-1,0.5) $ dans $ \mathbb{R} $ donne : $$ (-1,0.5) \cap [0,1] = [0,0.5) $$ Cet intervalle est donc ouvert dans le sous-espace $ Y $, bien qu’il ne le soit pas dans $ \mathbb{R} $.

Il existe également des ensembles ouverts à la fois dans $ X $ et dans $ Y $, comme $ (0.2, 0.8) $.

De même, certains ensembles comme $ [0.2, 0.8] $ sont fermés dans les deux topologies.

Dans la topologie induite sur $ Y = [0, 1] $, l’ensemble $ [0, 1] $ est à la fois ouvert et fermé.

Ouvert
Pour montrer que $ [0, 1] $ est ouvert dans le sous-espace $ Y $, il suffit de prendre un ouvert $ U $ de $ \mathbb{R} $ tel que $ U \cap Y = [0, 1] $. En prenant $ U = \mathbb{R} $, on a : $$ U \cap Y = \mathbb{R} \cap [0, 1] = [0, 1] $$ Ainsi, $ [0, 1] $ est ouvert dans $ Y $.
Fermé
Pour démontrer que $ [0, 1] $ est fermé dans $ Y $, il suffit de le voir comme intersection de $ [0, 1] $, fermé dans $ \mathbb{R} $, avec lui-même : $$ [0, 1] \cap [0, 1] = [0, 1] $$
Remarque : On peut aussi conclure que $ [0, 1] $ est fermé dans $ Y $ car son complémentaire dans $ Y $ est l’ensemble vide, qui est toujours ouvert. Par conséquent, $ [0, 1] $ est fermé comme complémentaire d’un ouvert.

En conclusion, dans la topologie induite sur $ Y = [0, 1] $, l’ensemble $ [0, 1] $ est à la fois ouvert et fermé.

Un tel ensemble est appelé un ensemble « clopen », contraction des mots « closed » et « open ».

Exemple 2

Considérons la topologie usuelle sur l’ensemble $ \mathbb{R} $.

Dans cette topologie, tout intervalle ouvert $ (a,b) $ avec $ a < b $ est un ouvert.

L’ensemble des entiers $ \mathbb{Z} $ forme un sous-espace topologique de $ \mathbb{R} $, car chaque entier peut être obtenu comme intersection d’un intervalle ouvert de $ \mathbb{R} $ avec $ \mathbb{Z} $.

Par exemple, l’entier 7 s’écrit comme :

$$ (6.5,7.5) \cap \mathbb{Z} = \{ 7 \} $$

Et cela vaut pour tout entier.

Ainsi, tout singleton d’entier est un ouvert dans la topologie induite sur $ \mathbb{Z} $.

De même, tout sous-ensemble de $ \mathbb{Z} $ est également ouvert dans ce sous-espace.

Par exemple, pour obtenir l’ensemble $ \{6,7,8\} $, on intersecte :

$$ (5.5,8.5) \cap \mathbb{Z} = \{ 6, 7, 8 \} $$

La topologie induite sur $ \mathbb{Z} $ coïncide ainsi avec la topologie discrète.

Remarque : La topologie discrète sur $ \mathbb{Z} $ n’est pas une sous-topologie de celle de $ \mathbb{R} $, mais une topologie propre. Toutefois, la topologie induite sur $ \mathbb{Z} $ par celle de $ \mathbb{R} $ lui est équivalente.

Exemple 3

Considérons l’espace euclidien tridimensionnel $ \mathbb{R}^3 $, muni de la topologie usuelle, dans laquelle les ouverts sont les unions de boules ouvertes.

On s’intéresse à présent à la sphère unité $ S^2 $, définie comme l’ensemble des points de $ \mathbb{R}^3 $ situés à une distance égale à 1 de l’origine :

$$ S^2 = \{ (x, y, z) \in \mathbb{R}^3 \mid x^2 + y^2 + z^2 = 1 \} $$

La topologie induite sur $ S^2 $ est donnée par :

$$ T_{S^2} = \{ U \cap S^2 \mid U \text{ est ouvert dans } \mathbb{R}^3 \} $$

Autrement dit, un ensemble $ V \subseteq S^2 $ est ouvert dans la topologie induite si, et seulement si, il peut s’écrire comme l’intersection de $ S^2 $ avec un ouvert $ U $ de $ \mathbb{R}^3 $.

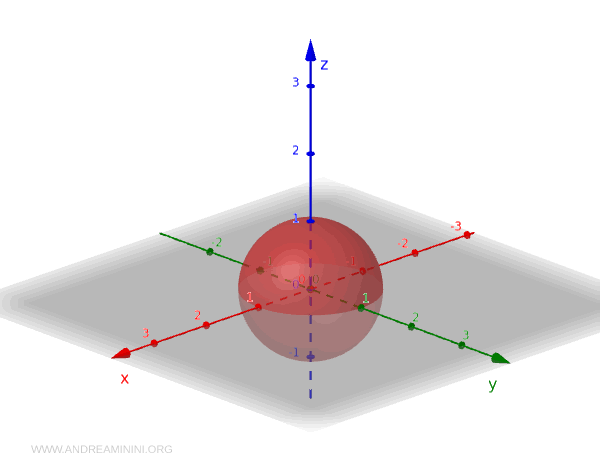
the sphere as a subspace

Voici quelques exemples typiques d’ouverts de $ S^2 $ :

Intersection avec un ouvert contenant la sphère entière
Soit $ U = \{ (x, y, z) \in \mathbb{R}^3 \mid x^2 + y^2 + z^2 < 2 \} $. Son intersection avec $ S^2 $ donne : $$ U \cap S^2 = S^2 $$ puisque tout point de $ S^2 $ vérifie $ x^2 + y^2 + z^2 = 1 < 2 $. Ainsi, $ S^2 $ est ouvert dans sa topologie propre.
Une région ouverte de la sphère
Prenons $ U = \{ (x, y, z) \in \mathbb{R}^3 \mid x^2 + y^2 + z^2 = 1 \text{ et } z > 0 \} $. Il s’agit de l’hémisphère supérieur. On a : $$ U \cap S^2 = \{ (x, y, z) \in S^2 \mid z > 0 \} $$ Ce sous-ensemble correspond à la partie supérieure de la sphère et constitue un ouvert dans $ T_{S^2} $.
Structure topologique de $ S^2 $
Les ensembles $ \emptyset $ et $ S^2 $ sont ouverts dans $ S^2 $ par définition.
- L’intersection d’un nombre fini d’ouverts de $ S^2 $ est encore un ouvert de $ S^2 $.
- De même, l’union quelconque (finie ou infinie) d’ouverts dans $ S^2 $ reste ouverte.

En résumé, la sphère $ S^2 $, considérée comme sous-espace topologique de $ \mathbb{R}^3 $, hérite de la topologie usuelle par restriction, c’est-à-dire que ses ouverts sont les intersections de $ S^2 $ avec des ouverts de $ \mathbb{R}^3 $.

Propriétés de la topologie induite

Les propriétés fondamentales de la topologie de sous-espace sont les suivantes :

Ensembles ouverts
Tout ouvert de $ Y $ est de la forme $ U \cap Y $, avec $ U $ ouvert dans $ X $.
Ouvertures élémentaires
L’ensemble vide $ \emptyset $ et l’ensemble total $ Y $ sont toujours ouverts dans $ Y $ :
- $ \emptyset = \emptyset \cap Y $
- $ Y = X \cap Y $
Stabilité par intersection finie
L’intersection d’un nombre fini d’ouverts dans $ Y $ est encore un ouvert de $ Y $. Si $ V_1, \ldots, V_n $ sont ouverts dans $ Y $, alors : $$ V_1 \cap \cdots \cap V_n = (U_1 \cap Y) \cap \cdots \cap (U_n \cap Y) = (U_1 \cap \cdots \cap U_n) \cap Y $$ où chaque $ U_i $ est ouvert dans $ X $, et leur intersection l’est aussi.
Stabilité par union arbitraire
Toute union, même infinie, d’ouverts de $ Y $ est un ouvert dans $ Y $. Si $ V_\alpha $ est ouvert dans $ Y $ pour tout $ \alpha \in I $, alors : $$ \bigcup_{\alpha \in I} V_\alpha = \bigcup_{\alpha \in I} (U_\alpha \cap Y) = \left( \bigcup_{\alpha \in I} U_\alpha \right) \cap Y $$ avec chaque $ U_\alpha $ ouvert dans $ X $.

Remarques

Quelques précisions supplémentaires sur les sous-espaces topologiques :

La topologie usuelle sur un sous-ensemble $ Y \subseteq \mathbb{R}^n $ coïncide avec la topologie induite par $ \mathbb{R}^n $.
Exemple : Considérons $ Y = [-1,0) \cup (0,1] $, sous-ensemble de $ \mathbb{R} $. Dans la topologie usuelle sur $ Y $, les intervalles $ [-1,0) $ et $ (0,1] $ sont ouverts car ils s’obtiennent comme intersections de $ Y $ avec des ouverts de $ \mathbb{R} $. Par exemple : $$ (-1.5,0.5) \cap Y = [-1,0) $$ $$ (0,1.5) \cap Y = (0,1] $$ Ainsi, la topologie usuelle sur $ Y $ est équivalente à la topologie induite par celle de $ \mathbb{R} $. De plus, ces deux intervalles sont aussi fermés dans $ Y $ car leur complémentaire respectif y est ouvert : le complémentaire de $ [-1,0) $ est $ (0,1] $ et vice versa. Ces ensembles sont donc à la fois ouverts et fermés, autrement dit clopens.
Théorème de la base dans les sous-espaces
Ce théorème affirme que si $ B_X $ est une base pour la topologie sur un espace $ X $, alors l’ensemble des intersections $ B \cap Y $, avec $ B \in B_X $, forme une base $ B_Y $ pour la topologie induite sur $ Y $ : $$ B_Y = \{ B \cap Y \ | \ B \in B_X \} $$

Et ainsi de suite.