Théorème de la base dans la topologie induite
Soit un espace topologique \(X\) muni d’une base \( B_X \) - c’est-à-dire une collection d’ouverts qui engendre la topologie sur \(X\) - et soit \(Y\) un sous-ensemble de \(X\). Alors, la collection des ensembles de la forme \( B \cap Y \), pour \( B \in B_X \), constitue une base \( B_Y \) pour la topologie induite sur \(Y\) : $$ B_Y = \{ B \cap Y \ | \ B \in B_X \} $$
Exemple
Illustrons ce résultat avec un exemple simple.
Considérons l’espace topologique \( \mathbb{R} \) muni de sa topologie usuelle, dont une base est formée par les intervalles ouverts \((a, b)\), avec \( a < b \).
Soit maintenant \(Y = [0, 2]\) un sous-ensemble de \( \mathbb{R} \).
Nous cherchons une base pour la topologie induite sur \(Y\).
La base de la topologie usuelle sur \( \mathbb{R} \) est :
$$ B_{\mathbb{R}} = \{(a, b) \ | \ a, b \in \mathbb{R}, \ a < b \} $$
Remarque : Cette base est l’ensemble de tous les intervalles ouverts \((a,b)\) avec \(a < b\) réels. Tout ouvert de \( \mathbb{R} \) peut s’écrire comme une union (éventuellement infinie) de tels intervalles. Par exemple, l’ouvert (0,3) peut être exprimé comme \( (0,2) \cup (1,3) \), et (2,5) comme \( (2,4) \cup (3,6) \).
La base de la topologie induite sur \(Y\) est obtenue en prenant l’intersection de chaque intervalle ouvert de \( \mathbb{R} \) avec \(Y = [0,2]\) :
$$ B_Y = \{ (a, b) \cap [0, 2] \ | \ (a, b) \in B_{\mathbb{R}} \} $$
Voici quelques exemples d’éléments appartenant à \( B_Y \) :
Avec \( (a, b) = (-1, 1) \), on obtient :
$$ (-1, 1) \cap [0, 2] = [0, 1) $$
Donc \( [0, 1) \in B_Y \).
Avec \( (a, b) = (1, 3) \), on obtient :
$$ (1, 3) \cap [0, 2] = (1, 2] $$
Ainsi \( (1, 2] \in B_Y \).
Enfin, avec \( (a, b) = (0.5, 1.5) \), on a :
$$ (0.5, 1.5) \cap [0, 2] = (0.5, 1.5) $$
Cet intervalle appartient aussi à \( B_Y \). Et il en va de même pour d’autres cas.
Vérifions maintenant que \( B_Y \) constitue bien une base pour la topologie induite :
Soit \(W = (0.5, 1.5]\) un ouvert dans la topologie induite sur \(Y\).
Cet ensemble est ouvert dans \(Y\) car il existe un ouvert \(U\) dans \( \mathbb{R} \) tel que \(W = U \cap [0, 2]\). Par exemple, on peut prendre \(U = (0.5, 1.5]\).
$$ W = U \cap [0, 2] = (0.5, 1.5] \cap [0, 2] = (0.5,1.5] $$
Choisissons un point \(y \in W\), disons \( y = 1 \).
Comme \(U = (0.5, 1.5]\) est ouvert dans \( \mathbb{R} \), il existe un intervalle \( (a, b) \in B_{\mathbb{R}} \) tel que \( y \in (a, b) \subseteq U \).
Par exemple, prenons \( (a, b) = (0.8, 1.2) \).
L’intersection avec \(Y\) donne :
$$ (0.8, 1.2) \cap [0, 2] = (0.8, 1.2) $$
Donc, \( (0.8, 1.2) \in B_Y \) et \( y = 1 \in (0.8, 1.2) \subseteq W \).
On en conclut que tout point de \(W\) est contenu dans un élément de \( B_Y \) inclus dans \(W\), ce qui confirme que \( B_Y \) est une base pour la topologie induite sur \(Y\).
Démonstration
Soient \(X\) un espace topologique et \(Y \subset X\) un sous-ensemble.
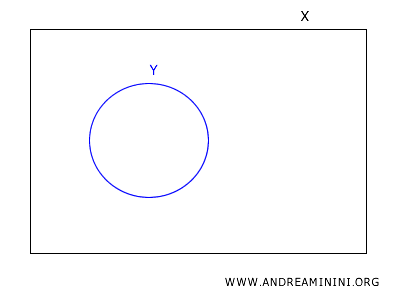
La famille \(B_Y\) est construite en prenant l’intersection de chaque élément de la base \(B_X\) avec \(Y\).
Chaque élément de \(B_Y\) est un ouvert dans la topologie induite sur \(Y\).
Il s’agit maintenant de montrer que cette famille \(B_Y\) constitue bien une base pour cette topologie.
Soit \(W\) un ouvert quelconque de la topologie induite sur \(Y\).
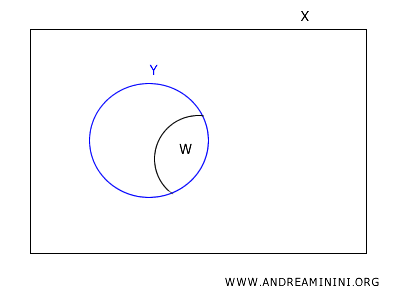
Par définition, il existe un ouvert \(U \subset X\) tel que \(W = U \cap Y\).
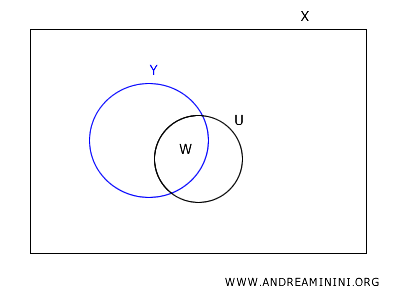
Soit \(y \in W\).
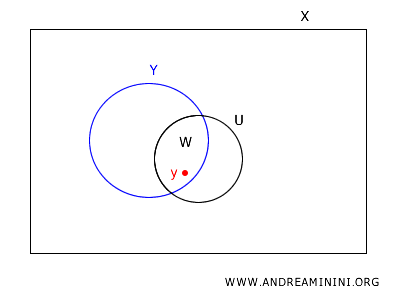
Comme \(U\) est ouvert dans \(X\), il existe un ensemble \(B \in B_X\) tel que \(y \in B \subseteq U\).
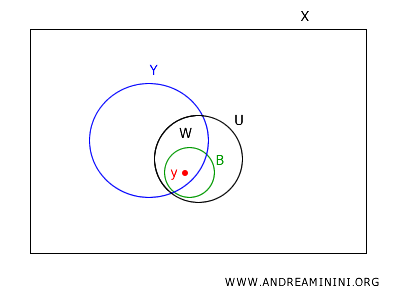
Alors \(B \cap Y\) est un élément de \( B_Y \) contenant \(y\) et inclus dans \(W\).
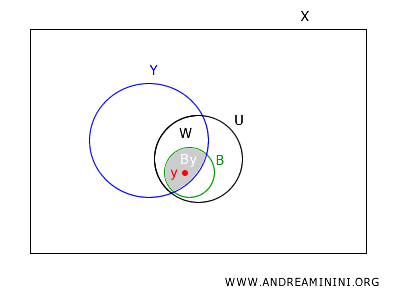
Par conséquent, tout point \(y \in W\) est contenu dans un élément de \(B_Y\) inclus dans \(W\).
$$ y \in B_Y = B \cap Y \subseteq U \cap Y = W $$
Cela démontre que \(B_Y\) forme une base pour la topologie induite sur \(Y\).
Et ainsi de suite.