Topologie discrète

La topologie discrète $ T $ est la topologie la plus fine que l’on puisse définir sur un ensemble $ X $, dans la mesure où elle contient l’intégralité de ses sous-ensembles.

Dans ce cadre, la famille des ouverts $ T $ englobe tous les sous-ensembles de $ X $. Ainsi, tout sous-ensemble de $ X $ est, par définition, un ensemble ouvert.

Il en résulte que chaque élément de $ X $ est un ouvert à part entière, ce qui implique que chaque point est isolé des autres.

En d’autres termes, il n’existe aucune contrainte de voisinage entre les éléments : toute configuration est envisageable.

Remarque. Une topologie sur un ensemble $ X $ est une collection de sous-ensembles de $ X $ (appelés « ouverts ») satisfaisant trois conditions fondamentales :

L’ensemble vide et l’ensemble $ X $ lui-même appartiennent à la collection $ T $.
Toute union arbitraire d’éléments de $ T $ appartient également à $ T $.
Toute intersection finie d’éléments de $ T $ appartient encore à $ T $.

On parle de topologie « discrète » car elle considère les éléments de $ X $ comme totalement distincts, sans la moindre notion de proximité ou de continuité entre eux.

Il s’agit de la topologie la plus riche que l’on puisse définir sur un ensemble, dans le sens où aucune autre topologie ne peut contenir davantage d’ouverts, puisque celle-ci les inclut tous.

Remarque. Ces conditions constituent le fondement de l’étude des ouverts, en fournissant un cadre formel pour analyser la manière dont les éléments d’un espace peuvent être perçus comme « proches » ou continus - une idée centrale pour comprendre le concept de continuité.

Une propriété essentielle de cette topologie est la suivante :

Dans la topologie discrète, tout sous-ensemble d’un espace topologique est à la fois ouvert et fermé.

Cette propriété découle du fait que tous les sous-ensembles de l’espace sont ouverts dans cette topologie.

Dès lors, le complémentaire de tout sous-ensemble de $ X $ est également un ouvert.

En topologie, un ensemble est dit fermé lorsque son complémentaire est un ouvert.

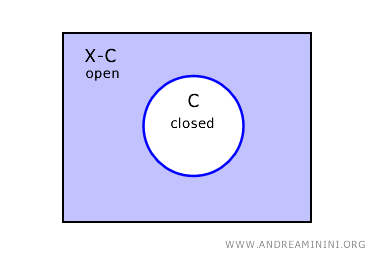
el complemento de un conjunto cerrado

Par conséquent, si le complémentaire de tout sous-ensemble est un ouvert, alors tous les sous-ensembles sont également fermés.

Ce trait distinctif de la topologie discrète implique que tout sous-ensemble est un ensemble clopen, c’est-à-dire à la fois ouvert et fermé, sans aucune exception.

Remarque. Dans la topologie discrète, cette propriété ne vaut pas seulement pour les points isolés, mais pour tout sous-ensemble. En effet, chaque point est un ouvert, de même que toute combinaison de points. Et puisque le complémentaire de tout sous-ensemble est également un sous-ensemble de $ X $, donc un ouvert, on en déduit que tout sous-ensemble est nécessairement fermé.

Un exemple concret

Illustrons la topologie discrète à l’aide d’un exemple simple, en considérant un ensemble fini $ X $ composé de trois éléments.

$$ X = \{a, b, c\} $$

L’ensemble des parties de $ X $, c’est-à-dire l’ensemble de tous ses sous-ensembles possibles, est constitué des éléments suivants :

L’ensemble vide : $\emptyset$
Les singletons : $\{a\}$, $\{b\}$, $\{c\}$
Les sous-ensembles à deux éléments : $\{a, b\}$, $\{a, c\}$, $\{b, c\}$
L’ensemble total : $\{a, b, c\}$

Dans la topologie discrète définie sur $ X $, chacun de ces sous-ensembles est un ouvert.

Ainsi, la topologie discrète $ T $ sur $ X $ est donnée par :

$$ T = \{\emptyset, \{a\}, \{b\}, \{c\}, \{a, b\}, \{a, c\}, \{b, c\}, \{a, b, c\} \} $$

Dans cette topologie, par définition, tous les sous-ensembles de $ X $ sont des ensembles ouverts.

Remarque. Cette famille constitue bien une topologie, puisqu’elle contient $ X $ et l’ensemble vide, et qu’elle est stable par unions arbitraires et intersections finies. Dans la topologie discrète, tous les sous-ensembles étant ouverts, aucune contrainte n’est imposée concernant la continuité ou la proximité des éléments de $ X $.

Considérons par exemple le sous-ensemble $ \{ a \} $. Selon la définition, il s’agit d’un ensemble ouvert.

Mais c’est aussi un ensemble fermé, puisque son complémentaire $ X \setminus \{a\} = \{b, c\} $ est également un ouvert. En topologie, rappelons-le, un ensemble est fermé si son complémentaire est ouvert.

On en conclut que, dans la topologie discrète, le sous-ensemble $ \{ a \} $ est à la fois ouvert et fermé.

Ce raisonnement s’applique à tout autre sous-ensemble de $ X $.

Et ainsi de suite.