Sous-ensembles Impropres
Qu’est-ce qu’un sous-ensemble impropre ?
On appelle sous-ensembles impropres ceux qui sont soit égaux à l’ensemble lui-même, soit réduits à l’ensemble vide.
Tout ensemble A possède toujours deux sous-ensembles impropres :
- l’ensemble identique à lui-même $$ A = A $$
- l’ensemble vide $$ Ø ⊂ A $$
Ensembles Égaux
Supposons que nous ayons deux ensembles égaux (A = B).
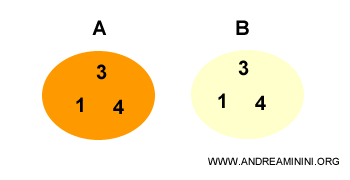
Chaque élément de l’ensemble A appartient également à l’ensemble B.
On en déduit que A est un sous-ensemble de B :
$$ A ⊆ B $$
De la même manière, chaque élément de B appartient aussi à A.
Donc, B est un sous-ensemble de A :
$$ B ⊆ A $$
Cette relation réciproque montre que les deux ensembles sont identiques.
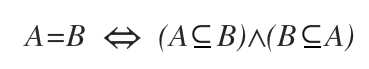
Ainsi, lorsque deux ensembles sont égaux (A = B), chacun est nécessairement sous-ensemble de l’autre.
Dans ce cas, on parle de sous-ensembles impropres, car ni A ni B ne peuvent être considérés comme des sous-ensembles propres l’un de l’autre.
Remarque. Un ensemble A est un sous-ensemble propre de B si tous les éléments de A sont contenus dans B, mais que B possède au moins un élément qui ne figure pas dans A. Cela n’est évidemment pas le cas lorsque les deux ensembles sont identiques.
Exemple
L’ensemble A est inclus dans B, et réciproquement :
$$ A = \{ 1,3,4 \} $$
$$ B = \{ 1,3,4 \} $$
Chaque élément de A appartient également à B, et chaque élément de B appartient aussi à A.
Par conséquent, ces deux ensembles sont des sous-ensembles impropres l’un de l’autre.
L’Ensemble Vide
Un ensemble est appelé ensemble vide lorsqu’il ne contient aucun élément.
On le note avec le symbole Ø : $$ Ø = \{ \ \ \} $$
L’ensemble vide est toujours considéré comme un sous-ensemble impropre de tout autre ensemble.
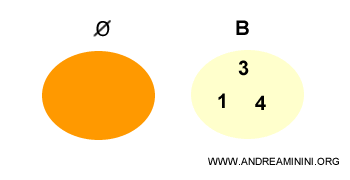
Remarque. Le fait que l’ensemble vide soit un sous-ensemble de tout ensemble peut sembler contre-intuitif, mais il se démontre rigoureusement (voir la démonstration). Voyons comment l’expliquer.
Exemple
Considérons l’ensemble vide et un ensemble quelconque A :
$$ Ø = \{ \ \ \} $$
$$ A = \{ 1,3,4 \} $$
L’ensemble vide Ø est inclus dans A :
$$ Ø ⊂ A $$
Pour le démontrer, supposons le contraire et essayons d’aboutir à une contradiction.
« L’ensemble vide N’EST PAS un sous-ensemble de A »
Si cela était vrai, il existerait au moins un élément dans l’ensemble vide qui ne se trouverait pas dans A.
Or c’est impossible, puisque l’ensemble vide ne contient aucun élément.
Par conséquent, l’affirmation « L’ensemble vide N’EST PAS un sous-ensemble de A » est fausse.
Si cette affirmation est fausse, alors son contraire, « L’ensemble vide EST un sous-ensemble de A », doit être vrai.
Démonstration Alternative. L’union d’un ensemble A avec l’un quelconque de ses sous-ensembles B ⊆ A donne toujours A lui-même : $$ A \cup B = A $$ Cela vaut également pour l’ensemble vide : $$ A \cup Ø = \{ 1,3,4 \} \cup \{ \ \ \} = \{ 1,3,4 \} = A $$