Union des intérieurs de deux ensembles
L’union des intérieurs de deux ensembles \( A \) et \( B \) est toujours incluse dans l’intérieur de leur union : \[ \text{Int}(A) \cup \text{Int}(B) \subseteq \text{Int}(A \cup B) \] Cependant, cette inclusion n’est pas nécessairement une égalité.
Autrement dit, l’intérieur de l’union est au moins aussi étendu que l’union des intérieurs.
Mais en général, ces deux ensembles ne coïncident pas. Il n’est donc pas toujours vrai que :
$$ \text{Int}(A) \cup \text{Int}(B) = \text{Int}(A \cup B) $$
L’inclusion peut très bien être stricte :
$$ \text{Int}(A) \cup \text{Int}(B) \ne \text{Int}(A \cup B) $$
Cette différence est fondamentale pour bien comprendre les interactions entre ensembles et intérieurs dans un cadre topologique.
Exemple illustratif
Considérons deux intervalles ouverts \( A \) et \( B \) dans \(\mathbb{R}\), muni de la topologie usuelle :
$$ A = (0, 2) \qquad B = (1, 3) $$
L’intérieur d’un intervalle ouvert étant lui-même, on a :
$$ \text{Int}(A) = (0, 2) \qquad \text{Int}(B) = (1, 3) $$
Leur union donne :
$$ \text{Int}(A) \cup \text{Int}(B) = (0, 2) \cup (1, 3) = (0, 3) $$
De même, l’union des ensembles \( A \cup B \) est :
$$ A \cup B = (0, 2) \cup (1, 3) = (0, 3) $$
Donc, leur intérieur est :
$$ \text{Int}(A \cup B) = \text{Int}((0, 3)) = (0, 3) $$
On obtient ainsi :
$$ \text{Int}(A) \cup \text{Int}(B) = \text{Int}(A \cup B) $$
Dans ce cas précis, l’égalité est vérifiée.
Considérons maintenant deux intervalles fermés : $$ A = [0, 2] \qquad B = [2, 3] $$ Leurs intérieurs sont : $$ \text{Int}(A) = (0, 2) \qquad \text{Int}(B) = (2, 3) $$ Tandis que leur union est \( A \cup B = [0, 3] \), dont l’intérieur est : $$ \text{Int}(A \cup B) = (0, 3) $$ L’inclusion suivante reste vraie : $$ (0, 2) \cup (2, 3) \subseteq (0, 3) $$ Mais l’égalité ne tient pas, car le point \( 2 \) appartient à l’intérieur de l’union : $$ 2 \in \text{Int}(A \cup B) = (0, 3) $$ alors qu’il n’appartient à aucun des deux intérieurs individuels : $$ 2 \not\in \text{Int}(A), \quad 2 \not\in \text{Int}(B) $$ Donc : $$ 2 \not\in \text{Int}(A) \cup \text{Int}(B) = (0, 2) \cup (2, 3) $$ On conclut que : $$ \text{Int}(A) \cup \text{Int}(B) \ne \text{Int}(A \cup B) $$ Ce contre-exemple confirme que l’inclusion peut être stricte.
Exemple 2
Considérons maintenant deux intervalles ouverts disjoints :
$$ A = (0, 1) \qquad B = (2, 3) $$
Leur intérieur est inchangé :
$$ \text{Int}(A) = (0, 1) \qquad \text{Int}(B) = (2, 3) $$
Donc l’union des intérieurs est :
$$ \text{Int}(A) \cup \text{Int}(B) = (0, 1) \cup (2, 3) $$
Et comme les ensembles \( A \) et \( B \) sont déjà ouverts, leur union est aussi ouverte :
$$ A \cup B = (0, 1) \cup (2, 3) \qquad \Rightarrow \qquad \text{Int}(A \cup B) = (0, 1) \cup (2, 3) $$
Dans ce cas également, on a égalité :
$$ \text{Int}(A) \cup \text{Int}(B) = \text{Int}(A \cup B) $$
Ces exemples dans \(\mathbb{R}\) montrent que l’union des intérieurs est toujours incluse dans l’intérieur de l’union. Mais seule une configuration particulière garantit que l’égalité est réalisée. Dès qu’il y a chevauchement aux frontières, une inclusion stricte peut apparaître.
Exemple 3
Considérons maintenant deux ensembles \( A \) et \( B \) dans le plan réel \(\mathbb{R}^2\), muni de la topologie usuelle.
Les ensembles \( A \) et \( B \) sont deux disques ouverts qui se recouvrent partiellement, centrés respectivement en \( (0, 0) \) et \( (0{,}5, 0) \), et de rayon \( 1 \) :
$$ A = \{ (x, y) \in \mathbb{R}^2 \mid x^2 + y^2 < 1 \} $$
$$ B = \{ (x, y) \in \mathbb{R}^2 \mid (x - 0{,}5)^2 + y^2 < 1 \} $$
Comme \( A \) et \( B \) sont ouverts, leur intérieur coïncide avec eux-mêmes :
$$ \text{Int}(A) = A \qquad \text{Int}(B) = B $$
L’union de leurs intérieurs est donc simplement l’union des deux disques :
$$ \text{Int}(A) \cup \text{Int}(B) = A \cup B $$
Cette union forme une région constituée des deux disques avec une zone de recouvrement partielle.
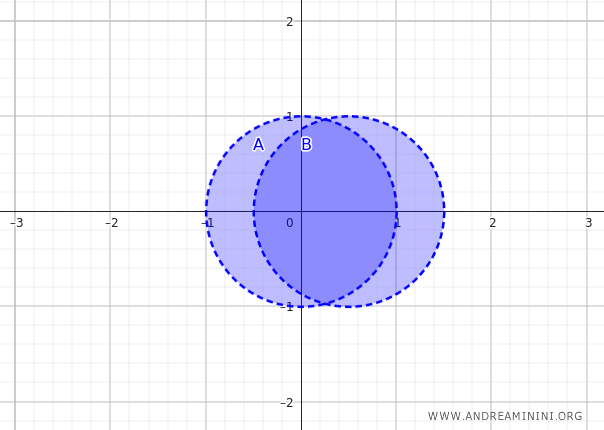
L’intérieur de l’union \( A \cup B \) est formé de tous les points qui possèdent un voisinage entièrement contenu dans \( A \cup B \) :
$$ \text{Int}(A \cup B) = A \cup B $$
On retrouve donc ici encore l’inclusion suivante :
$$ \text{Int}(A) \cup \text{Int}(B) \subseteq \text{Int}(A \cup B) $$
Démonstration de la propriété
Pour démontrer la propriété de l’union des intérieurs, il suffit de montrer que :
$$ \text{Int}(A) \cup \text{Int}(B) \subseteq \text{Int}(A \cup B) $$
Commençons par rappeler la définition de l’intérieur d’un ensemble.
L’intérieur d’un ensemble \( X \), noté \( \text{Int}(X) \), est l’ensemble des points \( x \in X \) pour lesquels il existe un ouvert contenant \( x \) et inclus dans \( X \).
Soit \( x \in \text{Int}(A) \cup \text{Int}(B) \). Alors \( x \in \text{Int}(A) \) ou \( x \in \text{Int}(B) \).
- Si \( x \in \text{Int}(A) \), il existe un ouvert \( U_x \) tel que \( x \in U_x \subseteq A \).
- Si \( x \in \text{Int}(B) \), il existe un ouvert \( V_x \) tel que \( x \in V_x \subseteq B \).
Dans les deux cas, comme \( A \subseteq A \cup B \) et \( B \subseteq A \cup B \), on a \( U_x \subseteq A \cup B \) ou \( V_x \subseteq A \cup B \). Cela signifie que \( x \in \text{Int}(A \cup B) \).
On en conclut que tout point de \( \text{Int}(A) \cup \text{Int}(B) \) appartient aussi à \( \text{Int}(A \cup B) \), ce qui démontre l’inclusion souhaitée :
$$ \text{Int}(A) \cup \text{Int}(B) \subseteq \text{Int}(A \cup B) $$
La démonstration est ainsi complète.