Método de los Multiplicadores de Lagrange

El método de Lagrange es una técnica muy eficaz para localizar los puntos críticos de una función de dos variables, $ f(x,y) $, cuando dichas variables están sujetas a una restricción.

En lugar de buscar extremos en todo el plano, limitamos la búsqueda al conjunto de puntos que cumplen la condición impuesta.

Este procedimiento nos permite encontrar extremos condicionados sin necesidad de parametrizar de forma explícita la restricción.

¿Cómo funciona?

Dada una función $ f(x, y) $ sometida a la restricción $ g(x, y) = 0 $, construimos una nueva función llamada Lagrangiano:

$$ L(x, y, \lambda) = f(x, y) + \lambda g(x, y) $$

Aquí, el parámetro $ \lambda $ recibe el nombre de multiplicador de Lagrange.

Para hallar los puntos críticos del Lagrangiano, calculamos sus derivadas parciales y las igualamos a cero. El resultado es el siguiente sistema:

$$
\begin{cases}
f_x(x,y) + \lambda g_x(x,y) = 0 \\
f_y(x,y) + \lambda g_y(x,y) = 0 \\
g(x, y) = 0
\end{cases}
$$

Aquí, $ f_x(x,y) = \frac{\partial f}{\partial x} $ y $ f_y(x,y) = \frac{\partial f}{\partial y} $ son las derivadas parciales de $ f $ respecto a $ x $ y $ y $.

El multiplicador $ \lambda $ es una incógnita adicional que puede adoptar valores positivos o negativos. Este sistema suele escribirse también en una forma equivalente, más simétrica:

$$
\begin{cases}
\frac{\partial f}{\partial x} = \lambda \frac{\partial g}{\partial x} \\
\frac{\partial f}{\partial y} = \lambda \frac{\partial g}{\partial y} \\
g(x, y) = 0
\end{cases}
$$

Resolver este sistema proporciona las coordenadas de los puntos críticos $ (x, y) $ sobre la curva de restricción, donde la función $ f(x, y) $ puede alcanzar un máximo o un mínimo local.

Una vez hallados estos puntos, es necesario determinar si corresponden a un máximo o a un mínimo. Hay dos métodos habituales:

• Evaluar $ f(x, y) $ en cada punto crítico y comparar los valores obtenidos.
• Analizar las condiciones de segundo orden mediante la matriz Hessiana.

En esencia, el método de Lagrange convierte un problema de optimización con restricciones en un sistema de ecuaciones que puede resolverse con las herramientas del cálculo diferencial.

Nota: Es fundamental que la restricción esté escrita en la forma estándar $ g(x,y)=0 $.

Un ejemplo resuelto

Consideremos la función:

$$ f(x, y) = 3x + 4y $$

sujeta a la restricción de que el punto se encuentre en una circunferencia:

$$ x^2 + y^2 = 25 $$

Como el método de Lagrange exige la restricción en la forma $ g(x,y)=0 $, la reescribimos así:

$$ x^2 + y^2 - 25 = 0 $$

Buscamos los puntos de la circunferencia $ x^2 + y^2 = 25 $ donde $ f(x, y) = 3x + 4y $ sea estacionaria, es decir, donde su variación en la dirección permitida se anule.

Construimos el Lagrangiano:

$$ L(x, y, \lambda) = 3x + 4y + \lambda(x^2 + y^2 - 25) $$

Calculamos las derivadas parciales y las igualamos a cero:

$$ \frac{\partial L}{\partial x} = 3 + 2\lambda x = 0 $$

$$ \frac{\partial L}{\partial y} = 4 + 2\lambda y = 0 $$

De aquí resulta el sistema:

$$ \begin{cases}
3 + 2\lambda x = 0 \\
4 + 2\lambda y = 0 \\
x^2 + y^2 = 25
\end{cases}
$$

Procedamos a resolverlo.

De la primera ecuación despejamos $ \lambda $:

$$ \lambda = -\frac{3}{2x} $$

Sustituyendo en la segunda:

$$ \begin{cases}
\lambda = -\frac{3}{2x} \\
\lambda = -\frac{2}{y} \\
x^2 + y^2 = 25
\end{cases} $$

Igualando las dos expresiones de $ \lambda $:

$$ -\frac{3}{2x} = -\frac{2}{y} \quad \Rightarrow \quad \frac{3}{2x} = \frac{2}{y} \Rightarrow 3y = 4x \Rightarrow y = \frac{4}{3}x $$

Sustituimos $ y = \frac{4}{3}x $ en la restricción:

$$ x^2 + \left(\frac{4}{3}x\right)^2 = 25 $$

$$ x^2 + \frac{16}{9}x^2 = 25 $$

$$ \frac{25}{9}x^2 = 25 $$

$$ x^2 = 9 \quad \Rightarrow \quad x = \pm 3 $$

Si $x = 3$, entonces $y = 4$; si $x = -3$, entonces $y = -4$.

Por tanto, los puntos estacionarios son $ P_1 = (3, 4) $ y $ P_2 = (-3, -4) $.

Para distinguir cuál corresponde al máximo y cuál al mínimo, evaluamos la función en ambos puntos:

$$ f(3, 4) = 3 \cdot 3 + 4 \cdot 4 = 9 + 16 = 25 $$

$$ f(-3, -4) = -9 - 16 = -25 $$

En consecuencia, $ P_1 = (3, 4) $ es el punto de máximo ( $ f(3,4) = 25 $ ), mientras que $ P_2 = (-3, -4) $ es el punto de mínimo ( $ f(-3,-4) = -25 $ ) bajo la restricción.

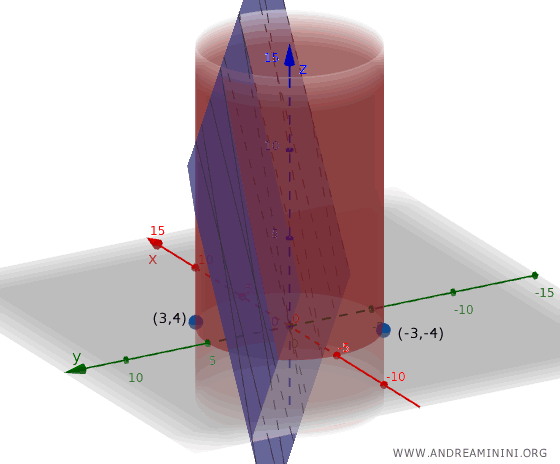
De este modo hemos identificado los puntos de la circunferencia en los que $f(x, y)$ alcanza su valor máximo y mínimo, utilizando únicamente ecuaciones y derivadas, sin necesidad de representar gráficamente la curva.

Evaluación del Hessiano Aumentado

Para determinar si los puntos críticos $ (3, 4) $ y $(-3, -4) $ corresponden a un máximo o a un mínimo, recurrimos a la matriz hessiana aumentada, que combina la información de la función objetivo con la de la restricción.

$$
H_L =
\begin{pmatrix}
L_{xx} & L_{xy} & g_x \\
L_{yx} & L_{yy} & g_y \\
g_x & g_y & 0
\end{pmatrix}
$$

Donde:

• $L_{xx} = \frac{\partial^2 L}{\partial x^2} = f_{xx} + \lambda g_{xx}$, y de forma análoga para los demás términos de segundo orden.
• $g_x = \frac{\partial g}{\partial x}$

Nota: El hessiano aumentado se diferencia del hessiano clásico, que se utiliza para estudiar la naturaleza de los puntos críticos en optimización sin restricciones. Este último solo depende de las segundas derivadas de la función $f(x, y)$: $$ H = \begin{pmatrix}
\frac{\partial^2 f}{\partial x^2} & \frac{\partial^2 f}{\partial x \partial y} \\
\frac{\partial^2 f}{\partial y \partial x} & \frac{\partial^2 f}{\partial y^2}
\end{pmatrix} $$ En cambio, el hessiano aumentado está diseñado para problemas con restricciones: incorpora las segundas derivadas de la función objetivo, las de la restricción y también las primeras derivadas de esta última, tal como aparecen en el Lagrangiano: $$
H_L =
\begin{pmatrix}
L_{xx} & L_{xy} & g_x \\
L_{yx} & L_{yy} & g_y \\
g_x & g_y & 0
\end{pmatrix}
$$

En este caso, calculamos las segundas derivadas parciales del Lagrangiano $ L(x, y, \lambda) = 3x + 4y + \lambda(x^2 + y^2 - 25) $, y de la restricción $ g(x,y) = x^2 + y^2 - 25 $:

$$ L_{xx} = 2 \lambda \quad L_{xy} = L_{yx} = 0 \quad L_{yy} = 2 \lambda $$

$$ g_{xx} = g_{yy} = 2 \quad g_{xy} = 0 $$

$$ g_x = 2x \quad g_y = 2y $$

Al sustituir estos valores en el hessiano aumentado, obtenemos:

$$ H_L = \begin{array}{ccc}
2\lambda & 0 & 2x \\
0 & 2\lambda & 2y \\
2x & 2y & 0
\end{array} $$

Evaluamos la matriz en cada punto crítico, introduciendo sus coordenadas y el valor correspondiente de $ \lambda $.

El paso siguiente es calcular el determinante. Un determinante positivo indica un máximo condicionado local, mientras que uno negativo señala un mínimo condicionado local.

1] Punto crítico (3, 4)

Obtenemos $ \lambda $ de la condición:

$$ 3 + 2\lambda \cdot 3 = 0 \quad \Rightarrow \quad \lambda = -\frac{1}{2} $$

Sustituyendo en la matriz:

$$
H_L =
\left|
\begin{array}{ccc}
-1 & 0 & 6 \\
0 & -1 & 8 \\
6 & 8 & 0
\end{array}
\right|
$$

Desarrollamos el determinante por la primera fila:

$$ \Delta H_L =
-1 \cdot
\left|
\begin{array}{cc}
-1 & 8 \\
8 & 0
\end{array}
\right|
- 6 \cdot
\left|
\begin{array}{cc}
0 & -1 \\
6 & 8
\end{array}
\right|
$$

$$ \Delta H_L = -1( -1 \cdot 0 - 8 \cdot 8 ) - 6( 0 \cdot 8 - (-1) \cdot 6 ) $$

$$ \Delta H_L = -1(-64) - 6(6) = 64 - 36 = 28 $$

El determinante resulta positivo, lo que confirma que $ (3, 4) $ es un máximo condicionado local.

2] Punto crítico (-3, -4)

Calculamos $ \lambda $ mediante:

$$ 3 + 2\lambda \cdot (-3) = 0 \quad \Rightarrow \quad \lambda = \frac{1}{2} $$

Al sustituir este valor en la matriz:

$$
H_L =
\left|
\begin{array}{ccc}
1 & 0 & -6 \\
0 & 1 & -8 \\
-6 & -8 & 0
\end{array}
\right|
$$

De nuevo desarrollamos por la primera fila:

$$ \Delta H_L = 1 \cdot
\left|
\begin{array}{cc}
1 & -8 \\
-8 & 0
\end{array}
\right|
- 6 \cdot
\left|
\begin{array}{cc}
0 & 1 \\
-6 & -8
\end{array}
\right|
$$

$$ \Delta H_L = 1( 0 - (-8)(-8) ) - 6( 0 - (-6) ) $$

$$ \Delta H_L = -64 - 36 = -100 $$

El determinante es negativo, lo que confirma que $ (-3, -4) $ corresponde a un mínimo condicionado local.

Este análisis con el hessiano aumentado respalda plenamente la clasificación que ya habíamos obtenido al evaluar directamente los valores de la función.

Ejemplo 2

Queremos determinar los valores mínimo y máximo de la función

$$ f(x,y) = x-2y $$

sujeta a la restricción de una circunferencia:

$$ g(x,y) = \{(x,y) \in \mathbb{R}^2 : x^2+y^2 \le 3 \} $$

Empezamos reescribiendo la restricción en la forma estándar $ g(x,y)=0 $:

$$ x^2+y^2 - 3 = 0 $$

Nuestra estrategia consiste en analizar la frontera de la región factible.

Para localizar los puntos candidatos donde puedan alcanzarse el mínimo y el máximo, intentamos primero resolver el siguiente sistema:

$$ \begin{cases} g_x(x,y) = 0 \\ g_y(x,y) = 0 \\ g(x,y)=0 \end{cases} $$

$$ \begin{cases} 2x = 0 \\ 2y = 0 \\ x^2+y^2 - 3=0 \end{cases} $$

$$ \begin{cases} x = 0 \\ y = 0 \\ x^2+y^2=3 \end{cases} $$

Este sistema no admite solución.

Por tanto, recurrimos al sistema que plantea el método de los multiplicadores de Lagrange:

$$ \begin{cases} f_x(x,y) = \lambda \cdot g_x(x,y) \\ f_y(x,y) = \lambda \cdot g_y(x,y) \\ g(x,y)=0 \end{cases} $$

$$ \begin{cases} 1 = 2 \lambda x \\ -2 = 2 \lambda y \\ x^2+y^2 - 3=0 \end{cases} $$

$$ \begin{cases} x = \frac{1}{2 \lambda} \\ y = - \frac{1}{ \lambda } \\ x^2+y^2 - 3=0 \end{cases} $$

$$ \begin{cases} x = \frac{1}{2 \lambda} \\ y = - \frac{1}{ \lambda } \\ \left( \frac{1}{2 \lambda} \right)^2+\left( - \frac{1}{ \lambda } \right)^2 =3 \end{cases} $$

$$ \begin{cases} x = \frac{1}{2 \lambda} \\ y = - \frac{1}{ \lambda } \\ \frac{1}{4 \lambda^2} + \frac{1}{ \lambda^2 } =3 \end{cases} $$

$$ \begin{cases} x = \frac{1}{2 \lambda} \\ y = - \frac{1}{ \lambda } \\ \frac{5}{4 \lambda^2} =3 \end{cases} $$

$$ \begin{cases} x = \frac{1}{2 \lambda} \\ y = - \frac{1}{ \lambda } \\ \lambda^2 = \frac{5}{12} \end{cases} $$

$$ \begin{cases} x = \frac{1}{2 \lambda} \\ y = - \frac{1}{ \lambda } \\ \lambda = \pm \frac{\sqrt{5}}{ 2\sqrt{3}} \end{cases} $$

Una vez determinado que $ \lambda = \pm \frac{\sqrt{5}}{ 2\sqrt{3}} $, sustituimos estos valores en las dos primeras ecuaciones para calcular las coordenadas de los puntos candidatos $(x,y)$.

Para $ \lambda = \frac{\sqrt{5}}{ 2\sqrt{3}} $:

$$ x = \frac{1}{2 \lambda} $$

$$ x = \frac{1}{2 \cdot \frac{\sqrt{5}}{ 2\sqrt{3}}} $$

$$ x = \frac{1}{\frac{\sqrt{5}}{ \sqrt{3}}} = \frac{ \sqrt{3} }{ \sqrt{5}} $$

$$ y = - \frac{1}{ \lambda } = - \frac{1}{ \frac{\sqrt{5}}{ 2\sqrt{3}} } = - \frac{ 2\sqrt{3} }{ \sqrt{5}} $$

Así, el primer punto candidato es $ (x,y)= \left( \tfrac{ \sqrt{3} }{ \sqrt{5}} , - \tfrac{ 2\sqrt{3} }{ \sqrt{5}} \right) $.

Para $ \lambda = - \frac{\sqrt{5}}{ 2\sqrt{3}} $:

$$ x = \frac{1}{2 \lambda} = \frac{1}{2 \cdot \left( - \tfrac{\sqrt{5}}{ 2\sqrt{3}} \right)} = - \frac{ \sqrt{3} }{ \sqrt{5}} $$

$$ y = - \frac{1}{ \lambda } = - \frac{1}{ - \tfrac{\sqrt{5}}{ 2\sqrt{3}} } = \frac{ 2\sqrt{3} }{ \sqrt{5}} $$

De este modo, el segundo punto candidato es $ (x,y)= \left( - \tfrac{ \sqrt{3} }{ \sqrt{5}} , \tfrac{ 2\sqrt{3} }{ \sqrt{5}} \right) $.

Sustituimos ahora estas coordenadas en la función $f(x,y)$ para determinar cuál corresponde al máximo y cuál al mínimo:

$$ f\!\left( \tfrac{ \sqrt{3} }{ \sqrt{5}} , - \tfrac{ 2\sqrt{3} }{ \sqrt{5}} \right) = \tfrac{ \sqrt{3} }{ \sqrt{5}} + \tfrac{ 4\sqrt{3} }{ \sqrt{5}} = \tfrac{5 \sqrt{3}}{ \sqrt{5} } = \sqrt{15} $$

$$ f\!\left( - \tfrac{ \sqrt{3} }{ \sqrt{5}} , \tfrac{ 2\sqrt{3} }{ \sqrt{5}} \right) = - \tfrac{ \sqrt{3} }{ \sqrt{5}} - \tfrac{ 4\sqrt{3} }{ \sqrt{5}} = - \tfrac{5 \sqrt{3}}{ \sqrt{5} } = - \sqrt{15} $$

Queda así demostrado que el valor máximo de $f(x,y)$ bajo la restricción $g(x,y)$ se alcanza en $ (x,y)= \left( \tfrac{ \sqrt{3} }{ \sqrt{5}} , - \tfrac{ 2\sqrt{3} }{ \sqrt{5}} \right) $, mientras que el valor mínimo se obtiene en $ (x,y)= \left( - \tfrac{ \sqrt{3} }{ \sqrt{5}} , \tfrac{ 2\sqrt{3} }{ \sqrt{5}} \right) $.

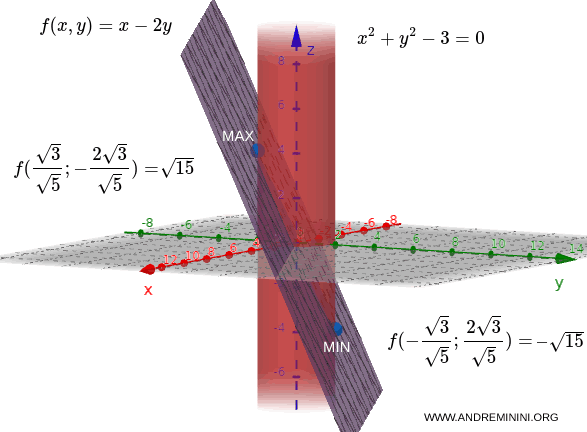
Y así sucesivamente.